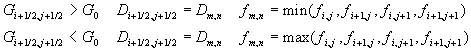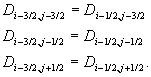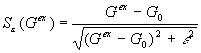7 Numerische
Verfahren
7.1 Einleitung
Neben den experimentellen und analytischen Methoden stehen
dem Ingenieur in zunehmendem Maße Simulationsrechnungen als Werkzeug bei der
Motorenentwicklung zur Verfügung. Dies ist durch die rasante Leistungssteigerung
der Digitalrechner in den letzten beiden Dekaden und durch die hierdurch
stimulierte Entwicklung genauer und schneller Algorithmen zur Lösung der
mathematischen Grundgleichungen bedingt. Es existieren eine Reihe von
Lösungsverfahren für inkompressible und kompressible Strömungen, die in der
einschlägigen Literatur wie etwa in [1],[2],[3],[4],[5],[6],[7]
beschrieben werden. Damit ist für die numerischen Forschungsarbeiten eine
sichere Basis vorhanden. Für selbstzuentwickelnde Programmpakete kann auf die
in Lehrbüchern oder in Fachzeitschriften veröffentlichten Artikel über
Lösungsverfahren zurückgegriffen werden, oder es können geeignete Programmpakete
auf dem Softwaremarkt erworben werden. Vor diesem Hintergrund konzentrieren
sich die numerischen Arbeiten auf die Ausarbeitung neuer mathematischer Modelle
für spezielle physikalische Vorgänge, wie zum Beispiel für die Strahlbildung
und den -zerfall bei Einspritzvorgängen. In besonderen Fällen jedoch müssen
ganz neue Lösungsmethoden entwickelt werden. Alle diese Wege sind im Rahmen der
in diesem Buch dokumentierten Forschungsarbeiten beschritten worden.
Neben selbstgeschriebener Software, Ergebnisse solcher
Untersuchungen sind in den Kapiteln 2 und 3 dokumentiert, wurden von den
Aachener Forschergruppen folgende Programmpakete im Rahmen des SFB verwendet:
SPICE, SPEED, KIVA II, Star-CD, FLUENT. Die Programmpakete wurden durch neue
Teilmodelle zur Lösung spezifischer Aufgaben erheblich erweitert und für die
Lösung besonderer Fragestellungen, wie die Berechnung des turbulenten Wärmeübergangs
im Motor, Kapitel 2.2.3.1, und
Strahlausbreitung, Zerstäubung und Verdampfung, Kapitel 4.2, oder Verbrennung im Dieselmotor, Kapitel 4.4.1.4, herangezogen. Die in diesen Computercodes implementierten
Lösungsalgorithmen hier näher zu beschreiben, würde den Umfang des Buches
sprengen. Für ein eingehendes Studium sei deshalb auf die in den genannten
Kapiteln aufgeführte Literatur verwiesen. Stattdessen sollen hier in einem
ersten Teil nur die Grundschritte zur numerischen Lösung partieller Differentialgleichungen
der Strömungsmechanik - die Formulierung des diskreten Problems - kurz
angerissen werden.
In einem zweiten Abschnitt, der das eigentliche Anliegen
dieses Kapitels ist, sollen dann zwei neuentwickelte Verfahren detaillierter
vorgestellt werden, deren Ausarbeitung nötig war, um die spezifischen
Eigenschaften der Interaktion von Strömung und Chemie bei der Ausbreitung
laminarer und turbulenter Vormischflammen numerisch mit ausreichender Genauigkeit
berechnen zu können. Diese Verfahren sind außer an dieser Stelle durch eine
Reihe von Veröffentlichungen [8],[9],[10],[11],[12],[13],[14] dokumentiert.
7.2 Erhaltungsgleichungen
Die mathematische Beschreibung der Transportvorgänge in
inerten und reaktiven Strömungen führt auf Erhaltungsgleichungen für
Vektorfelder. Die Änderung von physikalischen Größen in einem Gebiet t,
zusammengefaßt im Vektor  wird hervorgerufen
durch konvektive und diffusive tensorielle Flüsse
wird hervorgerufen
durch konvektive und diffusive tensorielle Flüsse 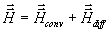 über die Oberfläche
des Gebietes und zum Beispiel durch Quellen und Senken im Inneren
über die Oberfläche
des Gebietes und zum Beispiel durch Quellen und Senken im Inneren 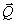 des Gebietes. Die
allgemeine mathehmatische Formulierung lautet mit dem nach außen gerichteten
Vektor
des Gebietes. Die
allgemeine mathehmatische Formulierung lautet mit dem nach außen gerichteten
Vektor 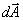 des Oberflächenelementes
des Oberflächenelementes
Gleichung 7-1: 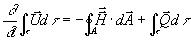 .
.
7.2.1 Konservative
und nichtkonservative Form
Bei Anwendung des Erhaltungssatzes auf Strömungen
reagierender Gase führt Gleichung
7-1 mit dem Vektor 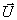 der konservativen Variablen
und den konvektiven und diffusiven Flüssen auf
der konservativen Variablen
und den konvektiven und diffusiven Flüssen auf
Gleichung 7-2: 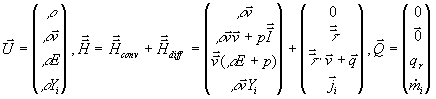 .
.
Darin bezeichnen r die Dichte, 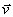 den
Geschwindigkeitsvektor,
den
Geschwindigkeitsvektor, 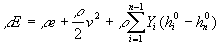 die spezifische
innere Totalenergie, p den Druck sowie
Yi die Massenbrüche und
die spezifische
innere Totalenergie, p den Druck sowie
Yi die Massenbrüche und 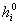 die
Bildungsenthalpien der Spezies i.
die
Bildungsenthalpien der Spezies i.
Der Vektor des Speziesdiffusionsstroms wird nach dem
Fickschen Gesetz
Gleichung 7-3: 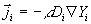
bestimmt. In dieser Formulierung sind
Thermodiffusionseffekte vernachlässigt und ein effektiver Diffusionskoeffizient
Di angenommen.
Der Wärmestrom q
errechnet sich aus dem Fourierschen Gesetz, Wärmeleitungskoeffizient k, und dem Enthalpietransport durch
Diffusion zu
Gleichung 7-4: 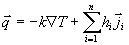 .
.
Für den chemischen Quellterm gilt
Gleichung 7-5: 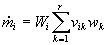 ,
,
worin Wi
die Molgewichte, 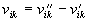 die stöchiometrischen
Nettokoeffizienten (netto) von Spezies i
in der Reaktion k mit der
Reaktionsrate wk bezeichnen.
die stöchiometrischen
Nettokoeffizienten (netto) von Spezies i
in der Reaktion k mit der
Reaktionsrate wk bezeichnen.
Für Newtonsche Fluide werden die Schubspannungen als
Funktion der Geschwindigkeitsgradienten
Gleichung 7-6: 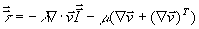
formuliert, wobei m den Viskositätskoeffizienten darstellt.
Nach einer Hypothese von Stokes ist der zweite Koeffizient l mit dem
Viskositätskoeffizienten durch l = -2/3m verknüpft.
Unter der Annahme eines lokalen thermodynamischen
Gleichgewichtes kann mit der Zustandsgleichung des idealen Gases
Gleichung 7-7: 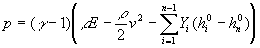
das Gleichungssystem geschlossen werden, wobei g =
cp/cv den Isentropenexponent bezeichnet.
Solange die durch Gleichung
7-1 beschriebenen Felder keine Diskontinuitäten ausbilden, lassen sich
mit dem Satz von Gauß für die obigen Integralgleichungen mathematisch äquivalente
partielle Differentialgleichungen aufschreiben. Diese lauten für kartesische
Koordinaten (x,y,z)
Gleichung 7-8: 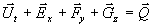
Beispielhaft steht der Term 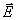 für
für
Gleichung 7-9: 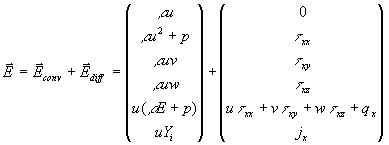 .
.
In dieser Form korrespondieren die partiellen
Differentialgleichungen (Gleichung
7-8) mit der allgemeinen Schreibweise eines Erhaltungsgesetzes (Gleichung 7-1);
daher wird diese Form die konservative oder Divergenzform genannt.
Alternativ können die konvektiven Anteile der Vektoren E, F und G des Erhaltungsgesetzes (Gleichung
7-8) in nichtkonservativer Form geschrieben werden, indem die
Ortsdifferentiationen ausgeführt werden und die Kontinuitätsgleichung
eingesetzt wird. Für die x-Komponente
des Impulssatzes folgt dann zum Beispiel:
Gleichung 7-10: 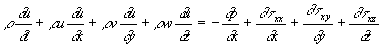 .
.
Beide Formulierungen sind nicht äquivalent, da die
nichtkonservative Formulierung sogenannte schwache Lösungen der
Erhaltungsgleichungen, also solche die Diskontinuitäten wie Stöße und
Vormischflammen enthalten, nicht einschließt.
7.2.2 Transformation
auf krummlinige, zeitabhängige Koordinaten
Mehrdimensionale Probleme gehen oft einher mit geometrisch
komplexeren Strömungsgebieten. Bei Motorinnenströmungen ist das
Integrationsgebiet zusätzlich durch die Bewegung von Kolben und Ventilen
zeitabhängig. Soll weiterhin die numerische Lösung der Erhaltungsgleichungen
auf kartesischen Gittern erfolgen, so müssen gesonderte Formalismen für die
Darstellung der Randbedingungen entworfen werden. Eine Alternative zu dieser Vorgehensweise
stellt die Formulierung der Erhaltungsgleichungen auf nichtstrukturierten
Netzen, die sich einer beliebigen Geometrie anzupassen vermögen oder auf
konturangepaßten Koordinaten dar.
Im Rahmen der hier durchgefürten Arbeiten ist stets der
zweite Weg beschritten worden. Dies erfordert eine Transformation der
Erhaltungsgleichungen auf ein zeitabhängiges, krummliniges, nichtorthogonales
Koordinatensystem, um den Aufwand bei der Formulierung der Randbedingungen in
Grenzen zu halten. Der physikalische Raum wird über die Transformation:
Gleichung 7-11: 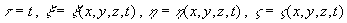
auf einen rechteckigen, äquidistanten und zeitabhängigen
Raum abgebildet. Mit dieser Vorschrift erhält man die transformierten
Navier-Stokes-Gleichungen
Gleichung 7-12: 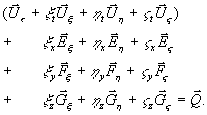
Diese nichtkonservative Form kann mit den Invarianten der
Koordinatentransformation wieder in eine konservative Form überführt werden
Gleichung 7-13: 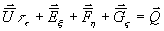 ,
,
mit 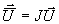 und zum Beispiel
und zum Beispiel 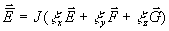 . Darin ist J die
Funktionaldeterminante der Transformation
. Darin ist J die
Funktionaldeterminante der Transformation
Gleichung 7-14: 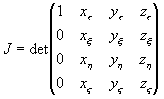 .
.
Diese Divergenzformulierung in krummlinigen Koordinaten ist
geeigneter Ausgangspunkt für die finite Differenzenformulierung der
Erhaltungsgleichungen.
Vielfach ist jedoch zu beobachten, daß diese Form formal auf
Strömungsprobleme mit zeitabhängigen Geometrien angesetzt wird, ohne zu
berücksichtigen, daß zur Erhaltung der konservativen Form die zeitabhängige
Invariante der Koordinatentransformation zu jedem Zeitpunkt erfüllt sein muß.
Auf diese Problematik hat erstmals Thomas in [15]
hingewiesen. Er bezeichnete diese Invariante, die eine Transportgleichung für
das Zellvolumen J darstellt, als
Geometric Conservation Law
Gleichung 7-15: 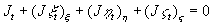 .
.
In Arbeiten von Tamura und Fujii [16]
wird die Notwendigkeit aufgezeigt, das Zellvolumen als Erhaltungsgröße zu betrachten.
In der numerischen Arbeit des Kapitels
2.1 wird Gleichung
7-15 als zusätzliche Erhaltungsgleichung analog zu den physikalischen Erhaltungsgleichungen
gelöst.
7.2.3 Anfangs-
und Randbedingungen
Das Gleichungssystem (Gleichung
7-8 bzw. Gleichung
7-13 einschließlich Gleichung
7-15) stellt ein Anfangswertporblem in der Zeit und ein Randwertproblem
im Ortsraum dar. Daher werden zur Lösung sowohl Anfangs- als auch
Randbedingungen benötigt, die problemabhängig zu formulieren sind und deshalb
hier nicht angegeben werden sollen.
7.3 Diskrete
Formulierung
Die numerische Lösung von partiellen Differential- oder
Integralgleichungen erfordert folgende Schritte:
·
die Definition des Gitters
·
die Approximation der Differentiale bzw. Integrale
durch algebraische Ausdrücke
·
ein Verfahren zur numerischen Lösung der algebraischen
Gleichungssysteme
Die folgenden Abschnitte sollen zu diesen Themen einen
kurzen Überblick bieten.
Für alle numerischen Lösungsverfahren, die im physikalischen
Raum operieren, muß das Integrationsgebiet, über dem die Lösung definiert ist,
diskretisiert werden. Für die abhängigen Variablen bedeutet dies, daß diese nur
auf den durch die Diskretisierung definierten Stützstellen bekannt sind, deren
Verteilung im physikalischen Raum das Gitter bzw. das Kontrollvolumen für die
Flußbilanzierung definiert. Dabei werden Verfahren danach unterschieden, wo die
abhängigen Variablen relativ zur Bilanzzelle gespeichert sind: „zellzentriert“
oder „eckenzentriert“. Inkompressible Lösungsverfahren [3]
verwenden oft eine Mischform, um die
Entkopplung von Druck- und Geschwindigkeitsfeld zu vermeiden („staggered
grids“). Wegen der Robustheit des Verfahrens bauen viele kommerzielle
Programmpakete auch zur Berechnung kompressibler Strömungen, wie KIVA II,
FLUENT, auf solche Gitter auf. Die verschiedenen Formulierungen haben Einfluß
auf den Abbruchfehler des numerischen Verfahrens (siehe auch Kapitel 7.2.2). Bei Verwendung nichtorthoganaler,
krummliniger Koordinaten und einer formalen Genauigkeit der diskreten Formulierung
von zweiter Ordnung auf othogonalen, äquidistanten Gittern ist lediglich eine
Genauigkeit von erster Ordnung erreichbar, da die Koeffizienten des nächst
höheren Terms der Taylorentwicklung nicht mehr exakt verschwinden [17].
Eine vergleichsweise genaue Approximation stellt zum Beispiel das
Cell-Vertex-Schema nach Hall [18]
dar.
7.3.2 Finite-Volumen-Verfahren
Finite Differenzen zur Approximation der Differentiale bauen
unmittelbar auf der Definition der Ableitung auf. Die Ableitung einer Funktion u am Punkt x ist durch
Gleichung 7-16: 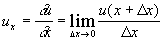
definiert. Falls Dx endlich bleibt, ist der Bruch auf der
rechten Seite eine mit abnehmendem Dx besser werdende Approximation zum
exakten Wert der Ableitung ux.
Die Differenz zwischen exakter Ableitung und ihrer Approximation wird
Abbruchfehler genannt, dessen Ordnung die Güte der Approximation bestimmt. Sie
läßt sich durch Einsetzen der Taylorentwicklungen für u(x+Dx) in die Differenzenformel und Vergleich mit der linken Seite
von Gleichung 7-16
ermitteln (Konsistenznachweis). Insbesondere müssen die verwendeten Gitter ein
hohes Maß an Regularität aufweisen, um den Abbruchfehler klein zu halten. Eine
solche Formulierung ist deshalb auf unstrukturierten Netzen nicht anwendbar.
Moderne Algorithmen gehen eher von einer finiten Volumenapproximation der
Erhaltungsgleichungen (Gleichung
7-1), die unmittelbar diskret formuliert wird, indem das Integral als diskretes
Kontrollvolumen aufgefaßt und die Bilanz für jede Gitterzelle des
Integrationsgebietes formuliert wird. Eine solche Vorgehensweise läßt
beliebigen Spielraum für die Anordnung der Kontrollzellen im
Integrationsgebiet. Das Ergebnis einer finiten Volumenapproximation der
Erhaltungsgleichungen stimmt mit der Differenzenapproximation überein, wenn die
Differenzenapproximation auf die differentielle Formulierung des
Erhaltungssatzes in konservativen Variablen angewandt wird.
Die Finite-Volumen-Methode ist Grundlage der diskreten
Formulierung aller hier verwendeten Näherungslösungen der
Differentialgleichungen. Eine ausführliche Darstellung zu diesem Gebiet findet
sich in [6].
7.3.3 Zeitliche
Integration und Operator-Splitting
Mit den in den beiden vorgehenden Abschnitten skizzierten
Vorgehensweisen sind die beiden Terme auf der rechten Seite von Gleichung 7-1
diskret formuliert. Die Berechnung der zeitlichen Evolution der
Erhaltungsgrößen führt auf eigene Techniken. Ausgangspunkt ist zunächst eine
Splitting-Technik, die näher erläutert werden soll.
Die Erhaltungsgleichungen der Strömungsmechanik bilanzieren
verschiedene physikalische Vorgänge wie Konvektion, Diffusion, Quellen mit
völlig unterschiedlichem mathematischen Charakter. So stellen die
reibungsfreien instationären und kompressiblen Eulergleichungen ein System
nichtlinearer, gekoppelter Differentialgleichungen vom hyperbolischen Typ dar,
wogegen z.B. die Diffusionsterme der Navier Stokes Gleichungen elliptischen
Charakter haben. Eine fortgeschrittene numerische Methodik berücksichtigt den
unterschiedlichen Charakter dieser Operatoren durch jeweils optimal angepaßte Algorithmen.
Die unterschiedlichen Integrationsmethoden zwingen daher die
zeitliche Entwicklung des Strömungsfeldes als überlagerten Effekt der
Einzelprozesse (Operatoren) darzustellen. Diese Zerlegung wird als
Operator-Splitting bezeichnet.
Dies sei anhand der reaktiven Eulergleichungen in zwei
Dimensionen
Gleichung 7-17: 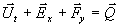
erläutert. Es wird eine Aufspaltung in die
richtungsabhängigen räumlichen Operatoren Lx
und Ly und den Operator
des Quellterms Lq
vorgenommen
Gleichung 7-18: 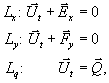
die den unterschiedlichen Eigenschaften des Quellterms und
der hyperbolischen Operatoren Rechnung trägt und zusätzlich berücksichtigt, daß
bisher keine zufriedenstellende Lösungsmethode für mehrdimensionale hyperbolische
Differentialgleichungen entwickelt werden konnte.
Die Lösung der Eulergleichungen in x-Richtung zum Beispiel wird dann zum Zeitpunkt t+Dt mit der diskreten Approximation 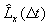 des Operators Lx aus
des Operators Lx aus
Gleichung 7-19: 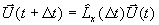
berechnet. Mehrere Operatoren erfordern deren
Hintereinanderschalten
Gleichung 7-20: 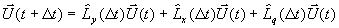 .
.
und ein Zwischenspeichern der Teilergebnisse 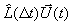 sowie nachträgliches
Summieren. Der zusätzliche Speicherbedarf kann vermieden werden, wenn die
Operatoren als Sequenz angewandt werden
sowie nachträgliches
Summieren. Der zusätzliche Speicherbedarf kann vermieden werden, wenn die
Operatoren als Sequenz angewandt werden
Gleichung 7-21: 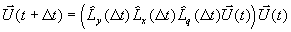 ,
,
wobei jedoch offensichtlich das Endergebnis von der
Reihenfolge der Anwendung der Operatoren abhängig ist. Die numerische
Approximation ist in diesem Fall nur von erster Ordnung, unabhängig ob die
Einzeloperatoren mit höherer Genauigkeit arbeiten.
Eine Splitting-Methode, die ohne zusätzlichen
Speicherplatzbedarf die Genauigkeit zweiter Ordnung eines numerischen
Integrationsverfahrens erhält, falls die Einzeloperatoren mindestens mit
zweiter Ordnung Genauigkeit formuliert werden, ist das Splitting nach Strang [19].
Es ermöglicht die Lösung des komplexen Gesamtproblems durch geeignete, geschachtelte
Abarbeitung der Teilprobleme in der Sequenz
Gleichung 7-22: 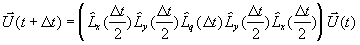
Sowohl die kommerziellen Codes, die im Rahmen von Teilprojekten
verwendet werden, als auch die Eigenentwicklungen an den verschiedenen Instituten
bedienen sich einer der obigen Formen des Operator-Splittings.
7.3.4 Stoßauflösende
Verfahren
Diskretisierung
Bei der Konstruktion von numerischen Verfahren für die
Eulergleichungen muß beachtet werden, daß wegen der Nichtlinearität der
Konvektionsterme diskontinuierliche Lösungen möglich sind. Soll mit Hilfe eines
numerischen Verfahrens die Bewegung der Diskontinuitäten richtig wiedergegeben
werden, ohne diese Bewegung gesondert im Algorithmus zu betrachten
(Shock-Capturing-Verfahren), so müssen zumindest die Ausbreitungsgeschwindigkeit
der Diskontinuität korrekt wiedergegeben, und unphysikalische Oszillationen in
der Nähe der Diskontinuität vermieden werden.
Das Näherungsverfahren
Gleichung 7-23: 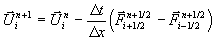
für Gleichung
7-18 bzw. Gleichung
7-19 heißt explizites Verfahren in Erhaltungsform und kommt einer
diskreten Integralform der Eulergleichungen, wie sie in Abbildung 7-1 dargestellt ist,
gleich.
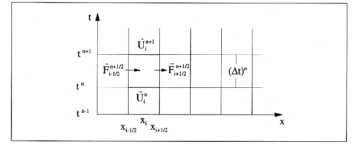
Abbildung 7-1:
Diskretisierung der 1-D Eulergleichungen in Raum und Zeit
Hier sind
Gleichung 7-24: 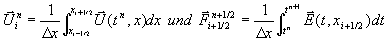
numerische Approximationen der Mittelwerte der
Erhaltungsgrößen 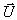 und der Flüsse
und der Flüsse 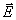 in x-Richtung auf den Rändern des
raumzeitlichen Gebietes [tn, tn+1]
x [xi-1/2, xi+1/2]
mit dem Zeitschritt Dt und der Zellgröße der Raumdiskretisierung
Dx
= xi+1/2 - xi-1/2. Zu jedem Zeitpunkt tn+1 wird der im Zellzentrum xi definierte neue
Zellmittelwert
in x-Richtung auf den Rändern des
raumzeitlichen Gebietes [tn, tn+1]
x [xi-1/2, xi+1/2]
mit dem Zeitschritt Dt und der Zellgröße der Raumdiskretisierung
Dx
= xi+1/2 - xi-1/2. Zu jedem Zeitpunkt tn+1 wird der im Zellzentrum xi definierte neue
Zellmittelwert 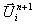 aus der Kenntnis des
alten Wertes
aus der Kenntnis des
alten Wertes 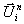 und den bei tn+1/2 zeitlich gemittelten
Flüssen
und den bei tn+1/2 zeitlich gemittelten
Flüssen 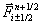 berechnet, die in
führender Ordnung nur die Näherungswerte von zwei Nachbarwerten
berechnet, die in
führender Ordnung nur die Näherungswerte von zwei Nachbarwerten 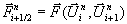 berücksichtigen. Eine
grundlegende Voraussetzung für Konvergenz des Näherungsverfahrens ist die
Konsistenz des numerischen Flusses, die besagt, daß der numerische Fluß
berücksichtigen. Eine
grundlegende Voraussetzung für Konvergenz des Näherungsverfahrens ist die
Konsistenz des numerischen Flusses, die besagt, daß der numerische Fluß 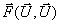 in den physikalischen
Fluß
in den physikalischen
Fluß 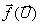 übergeht.
übergeht.
Aus der durch Gleichung
7-23 gegebenen konservativen Diskretisierung der Erhaltungsgleichungen
und der zusätzlichen Einhaltung der Konsistenzbedingung folgt nach [20], daß die
Rankine-Hugoniot-Bedingungen für die Näherungslösung erfüllt sind und die
Diskontinuität sich mit der exakten Ausbreitungsgeschwindigkeit bewegt.
Um ferner nur die physikalisch relevanten Lösungen zu
approximieren, muß neben der Erhaltungsform noch eine diskrete
Entropiebedingung erfüllt sein.
Die Vermeidung von Oszillationen in der Nähe großer Gradienten der Zustandsvariablen erfordert hingegen eine geeignete Auswertung
der Flußmittelwerte. Klassische zentrale Differenzenverfahren für 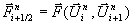 wie z.B. das
Zwei-Schritt-Lax-Wendroff-Verfahren [20]
weisen Oszillationen an Diskontinuitäten auf, die durch problemabhängig
anzupassende künstliche Dämpfungsterme beseitigt werden müssen [1].
wie z.B. das
Zwei-Schritt-Lax-Wendroff-Verfahren [20]
weisen Oszillationen an Diskontinuitäten auf, die durch problemabhängig
anzupassende künstliche Dämpfungsterme beseitigt werden müssen [1].
Bei modernen Shock-Capturing-Verfahren
(Godunov-Typ-Verfahren) resultieren die Dämpfungseigenschaften aus den
Welleneigenschaften der hyperbolischen Gleichungssysteme (siehe [21],[22],[23]).
Die grundlegende Idee der Godunov-Typ-Verfahren geht auf Godunov [24]
zurück. Er benutzte das Riemann-Problem, dessen inhärent nichtlineare
Lösungsstruktur aus Verdichtungsstößen, Expansionsfächern und
Kontaktunstetigkeiten aufgebaut ist, als einen Baustein für sein numerisches
Verfahren. Danach wird der numerische Flußmittelwert 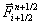 aus der Lösung des
Riemann-Problems der Gasdynamik in Abbildung
7-3 (links) mit konstanten Nachbarzuständen an der Zellgrenze xi+1/2
aus der Lösung des
Riemann-Problems der Gasdynamik in Abbildung
7-3 (links) mit konstanten Nachbarzuständen an der Zellgrenze xi+1/2
Gleichung 7-25: 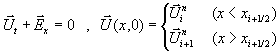
bestimmt zu
Gleichung 7-26: 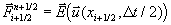 .
.
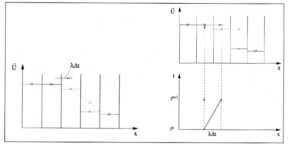
Abbildung 7-2:
Zentrale und upwind Diskretisierung
Der numerische Fluß erfährt sämtliche sprunghafte Änderungen
aufgrund der Wellenausbreitung und bezieht Informationen aus der
charakteristischen Richtung (upwind-biased Verfahren).
Die typische numerische Darstellung einer Diskontinuität ist
dann ein monotones Profil, wie es in Abbildung
7-2 (rechts) anhand der numerischen Lösung einer Stoßwelle dargestellt
ist. Es entstehen keine neuen, unphysikalischen Extremwerte, jedoch führt die
Monotonisierung des Zustandsverlaufs aufgrund der eingebrachten numerischen
Diffusion zu einer Verschmierung des ursprünglich scharfen Profils über zwei
bis vier Gitterpunkte.
Einer linearen Stabilitätsanalyse folgend, unterliegen die
so konstruierten expliziten Verfahren einer Zeitschrittbeschränkung, der
CFL-Bedingung
Gleichung 7-27: 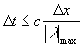 .
.
Sie besagt, daß die Welle mit der betragsgrößten
Ausbreitungsgeschwindigkeit lmax in einem Zeitschritt Dt
nicht so weit propagieren darf, daß die Flußberechnungen aus benachbarten
Riemann-Problemen jeweils voneinander abhängig sind; daher kann maximal c = 1 erlaubt werden.
Numerische Flüsse
Die Nachteile des Verfahrens von Godunov sind die
Genauigkeit von nur erster Ordnung und die Schwierigkeit, das nichtlineare
Riemann-Problem exakt zu lösen. Die exakte Lösung des Riemann-Problems
erfordert eine iterative Prozedur, welche zu einem relativ aufwendigen und
komplizierten numerischen Verfahren führt.
Godunov-Typ-Verfahren, wie z.B. von Roe [25], von Harten, Lax und van Leer [21]
oder von Harten, Lax
und van Leer mit der Modifikation nach Einfeldt [22], verwenden anstelle der exakten Lösung des
Riemann-Problems nur eine approximative nicht-iterative Lösung (Riemann-Löser).
Effiziente Riemann-Löser sind z.B. in [22]
und [25]
beschrieben.
Das in dieser Arbeit benutzte Verfahren beruht auf dem
approximativen Riemann-Löser von Roe [25].
Es gehört zu der Gruppe der Flux-difference-splitting-Verfahren und zerlegt die
Flußdifferenz zwischen den Anfangszuständen des Riemann-Problems in einzelne
Wellen (Abbildung
7-3).
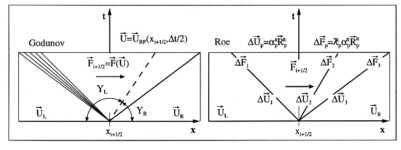
Abbildung 7-3:
Flußberechnung beim Verfahren von Godunov und von Roe
Approximativer Riemann-Löser nach
Roe
Bei diesem Verfahren wird das linearisierte Problem
Gleichung 7-28: 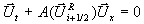
exakt nach der Charakteristikenmethode gelöst. Die
Gleichungen der Charakteristikentheorie gelten mit der Matrix A, die konsistent ist mit der Jakobischen
Matrix, ausgewertet in einem speziell gemittelten Zustand 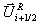 , der von den Nachbarzuständen
, der von den Nachbarzuständen 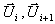 abhängt
abhängt
Gleichung 7-29: 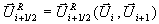 .
.
Der gemittelte Zustand 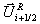 ist derart gewählt,
daß die Rankine-Hugoniot-Bedingungen zwischen den Nachbarzuständen
ist derart gewählt,
daß die Rankine-Hugoniot-Bedingungen zwischen den Nachbarzuständen
Gleichung 7-30: 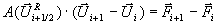
erfüllt sind und somit eine eindeutige Lösung über
Diskontinuitäten gewährleistet ist. Das nichtlineare Riemann-Problem wird für
einzelne stationäre Diskontinuitäten (Stoßwelle oder Kontaktunstetigkeit) somit
exakt gelöst. Durch die Erfüllung der Konsistenz der Matrix A folgen die reellen Eigenvektoren und
die Wellengeschwindigkeiten. Aufgrund der obigen Eigenschaften gelten die
allgemeinen Beziehungen:
Gleichung 7-31: 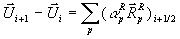 ,
,
Gleichung 7-32: 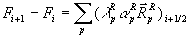 ,
,
wobei 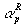 die Amplitude,
die Amplitude, 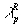 die
Wellengeschwindigkeit und
die
Wellengeschwindigkeit und 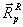 der Rechtseigenvektor
der p-ten Welle, ausgewertet im mittleren Zustand
der Rechtseigenvektor
der p-ten Welle, ausgewertet im mittleren Zustand 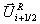 , sind. Die Flußdifferenz
, sind. Die Flußdifferenz 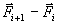 wird in die
Flußdifferenzen
wird in die
Flußdifferenzen 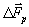 über den einzelnen
Wellen (Abbildung
7-3 rechts) aufgespaltet. Für den Flußvektor auf der Zellgrenze ergeben
sich nach dem Vorzeichen der Wellengeschwindigkeit die äquivalenten Beziehungen
über den einzelnen
Wellen (Abbildung
7-3 rechts) aufgespaltet. Für den Flußvektor auf der Zellgrenze ergeben
sich nach dem Vorzeichen der Wellengeschwindigkeit die äquivalenten Beziehungen
Gleichung 7-33: 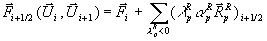 ,
,
Gleichung 7-34: 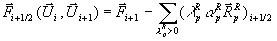 .
.
Roe benutzt den Mittelwert und formuliert den numerischen
Fluß erster Ordnung zu
Gleichung 7-35: 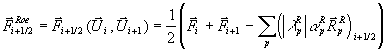 .
.
Zur Einhaltung der diskreten Entopiebedingung muß die
Ausbreitungsgeschwindigkeit l an sonischen Punkten in den
Expansionsfächern  derart modifiziert
werden, daß |l| > 0 ist. Die detaillierte Beschreibung dieses
sogenannten Entropie-Fixes findet man z.B. in [26].
derart modifiziert
werden, daß |l| > 0 ist. Die detaillierte Beschreibung dieses
sogenannten Entropie-Fixes findet man z.B. in [26].
Der Vektor der Wellenamplituden  ergibt sich aus
ergibt sich aus
Gleichung 7-36: 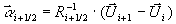 .
.
Die Rechtseigenvektoren und die Eigenwerte müssen in einem
gemittelten Zustand 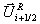 , dem Roe-Mittel, das speziellen mathematischen Bedingungen
genügen muß [25],
ausgewertet werden.
, dem Roe-Mittel, das speziellen mathematischen Bedingungen
genügen muß [25],
ausgewertet werden.
Fluß-und Steigungslimitierung
Das bisher beschriebene Verfahren nach Roe hat eine
Genauigkeit von erster Ordnung. Dagegen besitzt das Lax-Wendroff-Verfahren
einen Fluß zweiter Genauigkeitsordnung
Gleichung 7-37: 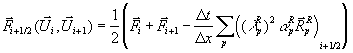 .
.
Berechnungen mit diesem Verfahren weisen jedoch in der Nähe
von Stößen unphysikalische Oszillationen auf. Um die Vorzüge des
Lax-Wendroff-Verfahrens und die oszillationsfreie Erfassung von
Diskontinuitäten durch die Flußformulierung erster Ordnung zu nutzen, wählt man
eine Kombination aus beiden, die in glatten Gebieten in den Lax-Wendroff-Fluß 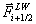 und an
Diskontinuitäten in den Roe-Fluß
und an
Diskontinuitäten in den Roe-Fluß 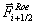 übergeht. In einer
Fluß-Limiter-Methode schreibt man den Fluß als Fluß erster Ordnung mit einem
limitierten Korrekturterm
übergeht. In einer
Fluß-Limiter-Methode schreibt man den Fluß als Fluß erster Ordnung mit einem
limitierten Korrekturterm
Gleichung 7-38: 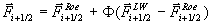 ,
,
wobei
Gleichung 7-39: 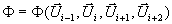
eine Limitierungsfunktion ist. In glatten Gebieten sollte
sie nahe 1 sein und an Diskontinuitäten nahe dem Wert 0. In der Anwendung
werden oft auch größere Wertebereiche von F zugelassen. Eine Klasse von
Fluß-Limiter-Methoden für skalare Erhaltungssätze wurde von Sweby [27]
untersucht. Algebraische Kriterien für die Limitierungsfunktion werden derart
angegeben, daß die zweite Genauigkeitsordnung und die TVD-Eigenschaft erfüllt sind.
Das Konzept der Total-Variation-Diminshing
(TVD) (Total-Variations-Vermindernden) Verfahren wurde von Harten [28]
eingeführt und besagt für skalare Erhaltungssätze, daß bei einem Zeitschritt 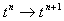 die Totalvariation
die Totalvariation 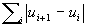 nicht zunimmt.
nicht zunimmt.
Die Übertragung auf Systeme geschieht durch die Betrachtung
der charakteristischen Amplituden der einzelnen Wellen. Umgeschrieben lautet
der Fluß
Gleichung 7-40: 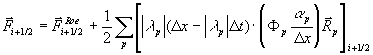
und mit der limitierten Steigung der charakteristischen
Wellenamplitude 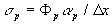
Gleichung 7-41: 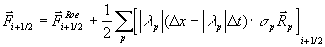
Die Limitierung läßt sich im Vergleich zum Roe-Fluß in einer
Korrektur der Wellenamplitude 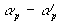 mit
mit 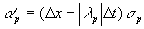 schreiben
schreiben
Gleichung 7-42: 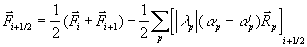 .
.
Der Wert der limitierten Steigung sp ist im
Zellzentrum definiert und ihr Wert an der Zellgrenze hängt von der
Ausbreitungsgeschindigkeit der betrachteten Welle ab:
Gleichung 7-43: 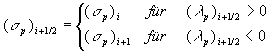
Der Vektor der Steigungen im Zellzentrum ist eine Funktion
ihrer benachbarten Steigungen an den Zellgrenzen. Die Limitierung kann in den
einzelnen Charakteristikenfeldern individuell gestaltet werden.
Für weitere Einzelheiten kann die bereits zitierte
einschlägige Literatur herangezogen werden.
7.4 Zwei
neue Algorithmen zur Simulation der Ausbreitung von Vormischflammen
Den im folgenden beschriebenen numerischen Algorithmen wird
eine Modellierung der Flammenausbreitung zugrundegelegt, die bewußt auf eine
detaillierte Auflösung der Flammenzone verzichtet.
Eine nähere Betrachtung der reaktiven Eulergleichungen
zeigt, daß Anfangs- und Randbedingungen zusammen mit den Rankine-Hugoniot
Sprungbedingungen an der Flammendiskontinuität für die korrekte Berechnung der
Flammenausbreitung nicht ausreichen [29],
da die Laxsche Entropiebedingung verletzt ist. Es fehlt die Festlegung der
Brenngeschwindigkeit als Funktion des Gaszustandes im Verbrannten. In den
nachfolgend beschriebenen numerischen Verfahren wird die
Flammenausbreitungsgeschwindigkeit deshalb als zusätzlicher Eingabeparameter
vorgeschrieben. Die Festlegung der Flammenausbreitungsgeschwindigkeit in
Abhängigkeit vom lokalen Strömungszustand und Reaktionsumsatz stellt eine wesentliche
Aufgabe der Modellbildung dar und ist in Kapitel
3.3 bereits eingehend dargestellt worden.
Die größten numerischen Schwierigkeiten bei der Lösung der
Eulergleichungen resultieren aus der Nichtlinearität der konvektiven Terme.
Moderne numerische Algorithmen, wie das im vorigen Abschnitt beschriebene,
bauen zur Lösung der Eulergleichungen auf sogenannten Capturing-Verfahren auf.
Durch ihre Konstruktion, sie gehen stets von der konservativen Form der
Eulergleichungen aus und garantieren dadurch die Erhaltungseigenschaften der
Differentialgleichungen auch in der diskreten Formulierung, werden die Lage und
die Ausbreitungsgeschwindigkeit von Kontaktdiskontinuitäten und Stößen richtig
wiedergegeben, ohne daß an den Fronten zusätzliche algorithmische Schritte
notwendig werden. Die Diskontinuitäten werden lediglich über einige Gitterpunkte
verschmiert wiedergegeben, wobei die Verschmierung vom speziellen numerischen
Verfahren abhängt. Für die Berechnung von Flammendiskontinuitäten kann aber
diese Verschmierung der Front nicht hingenommen werden, da eine korrekte
Auswertung des Brenngesetzes, das die Kenntnis von unverbrannten oder
verbranntem Gaszustand unmittelbar an der Flammenfront voraussetzt, nicht
vorgenommen werden kann. Die naive Anwendung von Capturing-Verfahren würde die
Flammenausbreitung an die spezifischen Eigenschaften des numerischen Verfahrens
bei der Darstellung der Flammenfront unzulässig koppeln.
Prinzipiell besser geeignet zur Berechnung der Ausbreitung
der Flammenfront sind demgegenüber sogenannte Tracking-Verfahren, die durch
spezielle Rechenschritte eine scharfe Wiedergabe von Diskontinuitäten erlauben.
Eine ganze Reihe von Verfahren sind gebräuchlich und in der wissenschaftlichen
Literatur dargestellt. Wesentlicher Nachteil dieser Verfahren ist die
programmtechnische Komplexität des Frontverfolgungsalgorithmusses, insbesondere,
wenn zwei- oder sogar dreidimensionale Problemstellungen gelöst werden sollen.
So arbeiten Tracking-Verfahren meistens auf numerischen Gittern, die sich der
verfolgenden Diskontinuität ganz oder zumindest teilweise anpassen. Dabei wird
das angepaßte Gitter bei starker Verformung der Diskontinuität ebenfalls stark
verformt. Das verwendete numerische Verfahren büßt dadurch an Genauigkeit ein.
Um diesen Nachteil in Grenzen zu halten und Singularitäten im Gitter zu
vermeiden, werden die Gitter häufig nach jedem Zeitschritt umverteilt, wodurch
neben dem algorithmischen Aufwand auch Interpolationsfehler in Kauf genommen
werden müssen.
Diese Schwierigkeiten und Nachteile von Tracking-Verfahren
können vermieden werden, wenn nur die nichtverzichtbaren Elemente eines solchen
Verfahrens in einen üblichen Algorithmus auf Basis eines Capturing-Verfahrens
auf festen Gittern übernommen werden. Unter diese Methoden, die die Fronten
innerhalb einer festen Gitterzelle approximieren, fallen die
Volume-of-Fluid-Methode, die Benutzung von Marker-Partikeln entlang der Front
und die Benutzung von Level-Sets zur Darstellung der Front. Eine Übersicht dazu
findet sich bei Hyman [30].
Im Rahmen des SFB 224 sind zwei Lösungsansätze erarbeitet
worden, die die Berechnung der Flammenausbreitung in mehreren Dimensionen zum
Ziel haben. Der erstere gehört zu der Klasse der Volume-of-Fluids-Methoden, der
zweite zu den auf Level-Sets aufbauenden Verfahren.
In beiden Lösungsansätze müssen folgende grundlegende
algorithmische Aufgaben bewältigt werden:
·
Rekonstruktion der Front
·
Konvektiver Transport der Front
·
Berechnung der lokalen Frontkrümmung,
wobei sich die Lösungsansätze im Detail unterscheiden. Eine
zusammenfassende Darstellung wird in den folgenden Abschnitten gegeben.
Als Voraussetzung zur Lösung der zuerst genannten
Teilaufgabe werden in beiden Lösungsansätzen zur geeigneten Darstellung der
Front eine Gewichtsfunktion eingeführt, indem für jede Zelle i,j des Rechengitters ein Volumenanteil fij definiert wird, der
angibt, welcher Anteil des Zellvolumens hinter der Front liegt. Die
Volumenverteilung ist die Gesamtheit der Volumenanteile in den einzelnen Zellen
und liefert die Informationen für eine vollständige Beschreibung der
Flammenkontur mit einer Genauigkeit, die größer als die Gitterauflösung ist.
Die Verfahren unterscheiden sich in der Art wie diese Volumenverteilung zu
jedem Zeitschritt des Rechenverfahrens erzeugt wird und wie diese Information
zur Rekonstruktion der Front umgesetzt wird.
7.4.1 Numerisches
Verfahren zur Berechnung der Flammenausbreitung mit der Volume-Of-Fluid-Methode
Zur Simulation des gesamten, mehrdimensionalen
Verbrennungsvorgangs im Verbrennungsraum wird bei diesem Front Tracking
Verfahren an Arbeiten angeknüpft, wie sie in [31],[32] dargestellt wurden. In diesen Arbeiten
wird eine unendlich dünne laminare Flammenfläche verfolgt und ihre Faltung
durch die Turbulenz mit dem Random-Vortex-Verfahren [33],[34],[35]
also einer Überlagerung der Grundströmung mit zufallsverteilten Wirbeln, realisiert.
In der vorliegenden Arbeit wird dagegen das Fortschreiten der turbulenten
Flamme als Zone mit gleichmäßig verteiltem Reaktionsumsatz betrachtet, ohne
ihre Struktur im Detail aufzulösen. Bei diesem Vorgehen wird berücksichtigt,
daß die turbulente Flammengeschwindigkeit eine Funktion der Turbulenzintensität
und der Zeit ist. Für die zeitliche Entwicklung der turbulenten
Flammengeschwindigkeit wurde die Abhängigkeit zugrundegelegt, wie sie in Gleichung 3.3-39 wiedergegeben ist. Von
einer Beschreibung der Struktur der Reaktionszone wurde wegen des zu
erwartenden hohen Rechenaufwandes zunächst abgesehen und das einfachere
Entrainment-Modell benutzt [36],[37].
Rekonstruktion der Front durch
Volume Of Fluid
Von Hirt und Nichols [38] wurde ein Algorithmus zur
Rekonstruktion einer Front unter dem Namen Volume Of Fluid (VOF) vorgestellt.
Dieses Verfahren wurde für Problemstellungen aus der Fluidmechanik entwickelt
und basiert auf der Annahme von zwei Fluiden, die durch eine Front voneinander
getrennt sind. Die Anteile der beiden Fluide in einer Zelle werden, wie
beschrieben, durch den Volumenanteil fij
repräsentiert.
Durch jede Zelle mit einem Volumenanteil zwischen 0 und 1
wird eine Gerade konstruiert, die die Zelle im Verhältnis der Volumenanteile
der Fluide b und u teilt. Die Steigung dieser Geraden ergibt sich aus einer
Betrachtung der acht Nachbarzellen. Anhand dieser Nachbarzellen wird auch
entschieden, auf welcher Seite der Geraden Fluid u bzw. Fluid b liegt.
Konvektion der Volumenverteilung
Der Algorithmus basiert auf dem von Poo und Ashgriz [39]
vorgeschlagenen Konvektionsalgorithmus und der von Hirt und Nichols [38]
vorgestellten Donor-Acceptor-Methode.
Die Verfahren werden zur Verwendung mit einer VOF-Rekonstruktion modifiziert.
Das Strömungsfeld wird als bekannt vorausgesetzt - repräsentiert durch die
Geschwindigkeitskomponenten -, wie in Abbildung
7-4 links für eine Zelle dargestellt.
Bei dem Algorithmus werden jeweils zwei benachbarte Zellen
betrachtet und der Fluß über die gemeinsame Grenze bestimmt. Die stromauf
gelegene Zelle ist die Donor-Zelle und die stromab gelegene Zelle ist die
Acceptor-Zelle. Im Gegensatz zu der Flußberechnung in [40] wird der Fluß hier nur durch die
Donor-Zelle bestimmt. Für die Berechnung des Flusses aus der Donor-Zelle wurde
die beschriebene VOF-Rekonstruktion zugrunde gelegt. Über eine rein geometrische
Betrachtung der Fläche des Verbrannten in der Donor-Zelle und der relevanten
Strömungskomponente läßt sich ermitteln, welcher Volumenanteil des Verbrannten
aus dieser Zelle pro Zeitschritt herausgetragen wird. Abbildung 7-4 rechts soll das Vorgehen
verdeutlichen. Darin beschreibt die geschwärzte Fläche den Fluß des Volumenanteils,
der während des Zeitschritts Dt zwischen beiden Zellen ausgetauscht
wird.
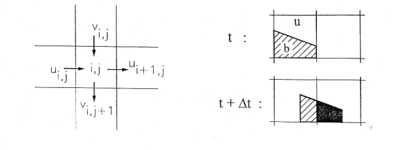
Abbildung 7-4:
Positionen der Geschwindigkeitsvektoren (links), Prinzip des Konvektionsalgorithmus
(rechts)
Für die Konvektionsberechnung der gesamten Volumenverteilung
wird eine Aufspaltung in die beiden Achsenrichtungen vorgenommen und die Konvektion
in diese beiden Richtungen nacheinander durchgeführt. Für eine Richtung werden
dann nacheinander alle möglichen Paare v
von benachbarten Zellen betrachtet und die jeweiligen Flüsse ausgewertet. Die berechneten
Flüsse werden jeweils vom Volumenanteil der Donor-Zelle subtrahiert und zum Volumenanteil
der Acceptor-Zelle hinzuaddiert. Nachdem diese Prozedur für eine Richtung
komplett durchgeführt worden ist, wird die Front neu rekonstruiert und der
Vorgang für die andere Richtung wiederholt.
Der Algorithmus weist erhebliche Verbesserungen gegenüber
herkömmlichen Algorithmen auf, wie Abbildung
7-5 zeigt. Als Testfall wurde eine kreisrunde Front einer Strömung unterworfen,
die eine Festkörperrotation beschreibt. Während die Konvektion mit Hilfe des
beschriebenen Algorithmus kaum zu Deformationen führt (rechts), wird der Kreis
bei Verwendung einer Vergleichsmethode, basierend auf einer SLIC-Rekonstruktion [40], erheblich entstellt
(links).
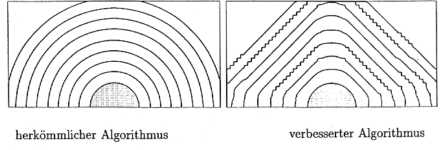
Abbildung 7-5:
Testrechnungen für Konvektionsalgorithmen
Zusätzlich zu dem soeben diskutierten rein passiven
Transport durch das Strömungsfeld, breitet sich eine Verbrennungsfront aktiv
relativ zum Hintergrundgas aus. Dabei verschiebt sich die Front im
Zeitintervall dt mit einer vorgegebenen
aktuellen Flammengeschwindigkeit sb
um den Betrag sb dt normal
zu sich selbst.
Die Normalenrichtung wird durch die VOF-Rekonstruktion für
jede Frontzelle direkt geliefert. Die durch die Frontverschiebung aufgespannte
Fläche - in Abbildung
7-6 schraffiert dargestellt - wird auf die überstrichenen Zellen entsprechend
des darin befindlichen Anteils aufgeteilt und führt auf eine neue
Volumenverteilung. Gleichzeitig kommt dieser Fläche bei der Bestimmung der
Quellenverteilung in der Strömungsberechnung Bedeutung zu.

Abbildung 7-6:
Prinzip des Ausbreitungsalgorithmus
Auch für die Ausbreitungsalgorithmen wurden Testrechnungen
durchgeführt. In Abbildung
7-7 wird eine kreisrunde Flamme betrachtet, die sich nach außen
ausbreitet und dabei keiner zusätzlichen Konvektion unterworfen ist. Die rechte
Seite zeigt Ergebnisse nach dem neuen Algorithmus, die Resultate auf der linken
Seite basieren auf dem SLIC-Algorithmus nach [33],[41].
|
herkömmlicher
Algorithmus
|
verbesserter
Algorithmus
|
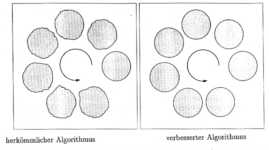
Abbildung 7-7:
Testrechnung für Ausbreitungsalgorithmen
Die Testrechnungen zeigen, daß der herkömmliche Algorithmus
die senkrechten bzw. waagerechten Richtungen bevorzugt, während die oben beschriebene
Methode keine solche Tendenz aufweist. Darüberhinaus sind die Ergebnisse des
herkömmlichen Algorithmus von der Zeitschrittweite abhängig.
Entrainment-Modell
Da nicht mehr eine unendlich dünne laminare Flammenfläche,
sondern eine Verbrennungszone mit endlicher Dicke betrachtet wird, muß jetzt
auch die Zeit berücksichtigt werden, die für die Umsetzung des eintretenden
Gases benötigt wird. Dazu wird ein Entrainment-Modell herangezogen [36],[37],[42].
Bei diesem Modell tritt das Frischgas in die Flammenzone in Form von
Volumenelementen einer charakteristischen Größe l ein. Diese Volumenelemente verbrennen an ihrer Oberfläche, wobei
eine laminare Flamme mit der laminaren Flammengeschwindigkeit sl nach innen fortschreitet.
Während dieses Verbrennungsvorganges wird das Volumenelement mit der Strömung
in der Brennkammer mitgeschleppt. Zum Zeitpunkt seines vollständigen Ausbrands
markiert jedes Element durch seine momentane Position einen Punkt der Flammenzonen-Rückfront.
Für die numerische Simulation ist es notwendig, das in einem
bestimmten Zeitschritt verbrennende Volumen zu kennen. Wie aus Abbildung 7-8
ersichtlich ist, nimmt der Radius des unverbrannten Kerns eines Volumenelementes
mit der Zeit ab:
Gleichung 7-44: 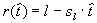
Hier bezeichnet 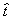 die seit dem Eintritt
in die Flammenzone verstrichene Zeit. Um das aktuelle Volumen
die seit dem Eintritt
in die Flammenzone verstrichene Zeit. Um das aktuelle Volumen 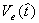 des Elementes zu
bestimmen, muß eine Annahme über seine geometrische Form getroffen werden.
des Elementes zu
bestimmen, muß eine Annahme über seine geometrische Form getroffen werden.
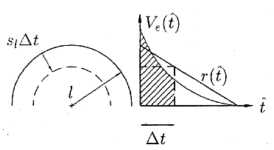
Abbildung 7-8:
Schematische Darstellung eines Volumenelementes aus dem Entrainment-Modell
Ashurst [43]
zeigt, daß unter gewissen Voraussetzungen zylindrische Strukturen in isotroper,
homogener Turbulenz besonders stabil sind, weshalb für die Simulationen von
einer Volumenabnahme des Unverbrannten entsprechend einer Zylindergeometrie
ausgegangen wird. Damit kann für jedes Volumenelement das aktuell verbrennende
Volumen bestimmt werden. Das insgesamt in einem Zeitschritt verbrennende
Volumen ergibt sich dann als Summe über alle aktiven Volumenelemente. Die
Änderung des unverbrannten Volumens eines Volumenelementes i in einem Zeitschritt ist ein direktes Maß für den lokalen Reaktionsumsatz
an der Position des Volumenelementes. Die Gesamtheit der Volumenelemente legt
damit die räumliche Verteilung des Umsatzes fest.
Modellierung des Strömungsfeldes
Für die Anwendung der Konvektionsalgorithmen ist die
Kenntnis des Strömungsfeldes erforderlich. Bei seiner Bestimmung wird
vorausgesetzt, daß die thermodynamischen Größen bereits bekannt sind. Das
Strömungsfeld wird wesentlich bestimmt durch die Expansion des Abgases.
Einem allgemein üblichen Ansatz bei
Front-Tracking-Anwendungen folgend [32],[44],[45],[46],
[47],[48]
wird die Strömung hier durch eine Potentialgleichung beschrieben. Das bedeutet,
daß Reibungs- und Wärmeleitungseffekte vernachläßigt werden und die Strömung
als drehungsfrei angesehen wird. Insbesondere die zuletzt genannte Einschränkung
kann bei Verwendung der Eulergleichungen aufgehoben werden - an ihrer
Implementierung in das Front-Tracking-Verfahren wird zur Zeit gearbeitet, um
Wirbelströmungen in der Brennkammer zu simulieren. Die hier vorgestellten
Rechnungen sollen jedoch auf Potentialströmungen beschränkt bleiben. Das
folgende Verfahren lehnt sich eng an das von Barr [31],[32],[41] vorgeschlagene an. Die
Strömung wird durch die Poissongleichung in der Form
Gleichung 7-45: 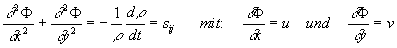
beschrieben. In dieser Gleichung bezeichnen F
das Geschwindigkeitspotential und sij
einen örtlich veränderlichen Quellterm, dessen Bestimmung im folgenden
erläutert wird. Durch geeignete Wahl dieses Quellterms läßt sich die zunächst
für inkompressible Strömungen formulierte Gleichung auch auf kompressible anwenden.
Ist das Potential als Lösung der Poissongleichung bekannt, so läßt sich das
Geschwindigkeitsfeld durch Differenzieren gewinnen. Die Quellstärke in einer
Zelle setzt sich aus drei Anteilen zusammen:
·
das Material, das im aktuellen Zeitschritt verbrennt,
expandiert und wirkt als Quelle
·
das Material, das im aktuellen Zeitschritt unverbrannt
bleibt, wird komprimiert und muß als Senke modelliert werden
·
das Material, das vor dem aktuellen Zeitschritt schon
verbrannt war, wird komprimiert und liefert ebenfalls einen Anteil als Senke.
Diese drei Punkte finden sich als Terme der folgenden
Formulierung für die Quellstärke unter Verwendung der Volumenanteile wieder:
Gleichung 7-46: 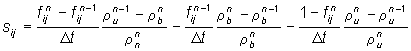
Hier bezeichnet n
den Zeitschritt. Äußerst wichtig ist die Plazierung der Quellen, die aktuell in
der Front neu entstanden sind. Um physikalisch sinnvolle Ergebnisse zu
bekommen, wurden diese Quellen eine Zelldiagonale hinter die Front verschoben,
um dann auf die vier nächsten Zellenmitten aufgeteilt zu werden. Die Aufteilung
erfolgt über eine Flächengewichtung, wie sie in Abbildung 7-9 verdeutlicht wird.
Aus der jeweiligen Teilfläche ergibt sich die Quellstärke, welche in der Zelle
gleichen Indexes positioniert wird. Diese Maßnahme sorgt dafür, daß die
Expansion immer im Verbrannten unmittelbar hinter der Front stattfindet, und
diese dann in die physikalisch einzig sinnvolle Richtung befördert wird.
Darüber hinaus ergibt sich noch ein gewisser Glättungseinfluß auf die sonst
recht instabile Front.
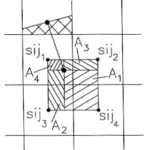
Abbildung 7-9:
Schematische Darstellung der Positionierung und der Verteilung der Quellterme
7.4.2 Erweitertes
Godunov-Typ-Verfahren zur Berechnung schneller Vormischflammen und des Deflagrations-Detonations-Übergangs
Das hier vorzustellende Verfahren gehört zu den
Level-Set-Verfahren zur Verfolgung von Diskontinuitäten in Strömungen. Die
Verwendung des Level-Set-Ansatzes wird durch das Flamelet-Modell für
Vormischflammen nahegelegt. Die in diesem Modell definierte Transportgleichung
für den Skalar G ist der Gleichung
für einen geeigneten Level-Set äquivalent, da definitionsgemäß eine Isolinie G = G0 der Hyperfläche 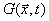 die momentane Lage
der Flammenfront repräsentiert.
die momentane Lage
der Flammenfront repräsentiert.
Zahlreiche Verfahren zum Verfolgen von Verdichtungsstößen
(siehe z.B. Chern und Colella [49])
und die Anwendung auf Stoßverfolgung bei der Simulation von Detonationen von
Bourlioux [50],[51])
und Kontaktunstetigkeiten (siehe z.B. den SLIC-Algorithmus [40]) wurden bereits
entwickelt. Flammen sind oft als „kalte", nicht-reaktive Fronten im Rahmen
von Level-Set-Ansätzen behandelt worden [52],[53]. Mangelhaft ist daran die fehlende
Interaktion zwischen Wärmefreisetzung und dem Strömungsfeld, der bei der
physikalischen Beschreibung eine zentrale Bedeutung zukommt.
Arbeiten, bei denen die Expansion des Gases aufgrund der
Flamme berücksichtigt wird, sind in [54],[55]
(level sets) und in [8]
(volume of fluid) veröffentlicht. In beiden Arbeiten wird ein Zwei-Zonen-Modell
verwendet, bei dem die Flamme verbranntes von unverbranntem Gas trennt. In den
zwei Zonen sind Druck, Dichte und Temperatur jeweils örtlich konstant und das
Geschwindigkeitsfeld wird durch eine quelltermbehaftete Potentialgleichung beschrieben.
Der Quellterm berücksichtigt die Expansion des Gases und die Druckerhöhung in
geschlossenen Behältern aufgrund der Wärmefreisetzung.
Der Nachteil dieser Formulierungen liegt in der Annahme der
örtlich konstanten Zustandsgrößen, die, besonders bei schnellen Flammen, nicht
mehr gewährleistet ist.
Wenn die reaktiven Eulergleichungen zur Berechnung der
Ausbreitung der diskontinuierchen Flammenfront herangezogen werden, fehlt, wie
im einleitenden Abschnitt bereits dargelegt, zur Berechnung der Ausbreitung von
Deflagrationen im Strömungsfeld eine Information, um das Gleichungssystem an
der Flammenfront zu schließen.
Für die auf Diffusion basierende Flamme muß die fehlende
Information durch die Vorgabe der Brenngeschwindigkeit su, die eine charakteristische Größe der Flammenstruktur
ist, eingeführt werden.
Als eine Konsequenz für die numerische Behandlung ergibt
sich die Notwendigkeit, einen unverbrannten Zustand 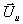 für die Auswertung
der Brenngeschwindigkeit
für die Auswertung
der Brenngeschwindigkeit 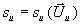 zu definieren. Ein
typisches Flammenprofil besitzt große Sprünge der Zustandsgrößen. Typische
Verhältnisse liegen bei
zu definieren. Ein
typisches Flammenprofil besitzt große Sprünge der Zustandsgrößen. Typische
Verhältnisse liegen bei
Gleichung 7-47: 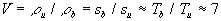 ,
,
wodurch wegen der unvermeidbaren numerischen Diffusion
unphysikalische Zwischenzustände produziert werden, die sich als Basis für die
Auswertung des Brenngesetzes verbieten. Eine scharfe Trennung zwischen
verbranntem und unverbranntem Zustand muß also gefordert werden. Die gasdynamische
Wechselwirkung zwischen Flamme und Strömungsfeld wird ohne über die Annahme
einer unendlich dünnen Flamme hinausgehende zusätzliche Vereinfachungen erfaßt.
Daher ist diese Formulierung insbesondere auch für schnelle Flammen geeignet
und erlaubt, den Übergang von Deflagration zu Detonation - ein wesentlicher
Mechanismus bei der klopfenden Verbrennung - numerisch zu simulieren. Der Zugang
zur Lösung dieser Aufgabenstellung basiert auf einem Flammen-Tracking, das in Anlehnung
an das Stoß-Tracking [56],[57],
basierend auf der Ausbreitung von Wellen nach LeVeque [58],[59],[60],
entwickelt wurde, und ein Flammen-Rekonstruktionsverfahren, welches auf der
Repräsentation der Deflagration durch die G-Gleichung
beruht. Beiden Verfahren ist gemeinsam, daß sie als
Wellenverteilungsalgorithmen geschrieben werden können.
Tracking durch Wellenverteilung
Ausgehend von der Wellendarstellung formulierte LeVeque ein
Tracking-Verfahren für die Behandlung von Stoßwellen. Die grundsätzliche Idee
ist es, eine starke Diskontinuität zu verfolgen und Anteile anderer schwacher
Wellen linear zu überlagern. Dort, wo die Flamme eine Zelle (i) im Punkt 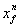 schneidet (die Zelle,
die die Flamme enthält, wird im folgenden die Mischzelle genannt), wird diese
in zwei Teilzellen (i)b im
Intervall
schneidet (die Zelle,
die die Flamme enthält, wird im folgenden die Mischzelle genannt), wird diese
in zwei Teilzellen (i)b im
Intervall 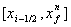 und (i)u in
und (i)u in 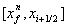 mit den
Zustandsvektoren
mit den
Zustandsvektoren 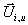 und
und 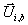 unterteilt. Durch
Verfolgung der einzelnen Wellen über Zellgrenzen hinweg, gelingt es, die aus
der CFL-Bedingung resultierenden sehr kleinen Zeitschrittweiten Dt = cDxmin/|l|max zu vermeiden.
unterteilt. Durch
Verfolgung der einzelnen Wellen über Zellgrenzen hinweg, gelingt es, die aus
der CFL-Bedingung resultierenden sehr kleinen Zeitschrittweiten Dt = cDxmin/|l|max zu vermeiden.
Die Wellen ergeben sich aus den gespeicherten verbrannten
und unverbrannten Zuständen der Teilzellen, mit denen das Flammen-Riemann-Problem
gelöst wird (Abbildung
7-10). Eine Beschreibung des hierzu notwendigen iterativen Verfahrens
wird z.B. in [61] gegeben.
Die gegebenen Zustände 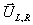 stellen die
Anfangsdaten dar. Gesucht wird der Druck pu
vor der Flamme, nachdem eine Stoßwelle oder ein Expansionsfächer über den
Zustand
stellen die
Anfangsdaten dar. Gesucht wird der Druck pu
vor der Flamme, nachdem eine Stoßwelle oder ein Expansionsfächer über den
Zustand 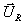 gelaufen ist. Mit dem
Druck pu ist über die
Stoßbedingung oder die isentropen Gleichungen für den Expansionsfächer der
unverbrannte Zustand
gelaufen ist. Mit dem
Druck pu ist über die
Stoßbedingung oder die isentropen Gleichungen für den Expansionsfächer der
unverbrannte Zustand 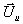 vor der Flamme
gegeben. Mit dem Zustand
vor der Flamme
gegeben. Mit dem Zustand 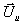 , dem Brenngesetz
, dem Brenngesetz 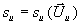 und den
Rankine-Hugoniot-Bedingungen für die Flamme folgt der verbrannte Zustand
und den
Rankine-Hugoniot-Bedingungen für die Flamme folgt der verbrannte Zustand 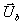 hinter der Flamme. Da
der Druck im verbrannten Zustand pb
über der Kontaktunstetigkeit konstant bleibt (pb = pS) folgt mit pS über die Stoßbedingungen oder die isentropen
Gleichungen für den linkslaufenden Expansionsfächer der Zustand
hinter der Flamme. Da
der Druck im verbrannten Zustand pb
über der Kontaktunstetigkeit konstant bleibt (pb = pS) folgt mit pS über die Stoßbedingungen oder die isentropen
Gleichungen für den linkslaufenden Expansionsfächer der Zustand 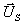 . Die Bedingung für die Konvergenz lautet dann, daß die
Geschwindigkeiten über der Kontaktunstetigkeit gleich bleiben (ub = uS), womit
das System iterativ gelöst werden kann.
. Die Bedingung für die Konvergenz lautet dann, daß die
Geschwindigkeiten über der Kontaktunstetigkeit gleich bleiben (ub = uS), womit
das System iterativ gelöst werden kann.
Aus der Lösung des Flammen-Riemann-Problems folgt mit der
Ausbreitungsgeschwindigkeit der Flamme Df
die neue Flammenposition zu 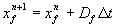 . Es sei angenommen, daß die Flamme in die Nachbarzelle (i+1) wandert. Die neue Mischzelle zum
Zeitpunkt tn wird
ebenfalls in zwei Teilzellen (i+1)b
im Intervall
. Es sei angenommen, daß die Flamme in die Nachbarzelle (i+1) wandert. Die neue Mischzelle zum
Zeitpunkt tn wird
ebenfalls in zwei Teilzellen (i+1)b
im Intervall 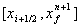 und (i+1)u in
und (i+1)u in 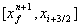 mit den
Zustandsvektoren
mit den
Zustandsvektoren 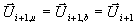 unterteilt. Die
geometrischen Verhältnisse sind in Abbildung
7-10: Flammen-Riemann-Problem
unterteilt. Die
geometrischen Verhältnisse sind in Abbildung
7-10: Flammen-Riemann-Problem
Abbildung 7-11 dargestellt. Zusätzlich zum Flammen-Riemann-Problem
an der Flammenposition 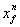 werden an den
Zellgrenzen xi-3/2, xi-1/2,
xi+1/2, xi+3/2 Roe-Riemann-Probleme gelöst. Die
einzelnen Wellen überstreichen während des Zeitschritts ein Volumen lpDt.
Der Wellensprung
werden an den
Zellgrenzen xi-3/2, xi-1/2,
xi+1/2, xi+3/2 Roe-Riemann-Probleme gelöst. Die
einzelnen Wellen überstreichen während des Zeitschritts ein Volumen lpDt.
Der Wellensprung 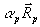 wird auf alle
teilweise oder ganz überstrichenen Zellen verteilt. Der Sprung der Flamme, wie
sie in Abbildung
7-11 dargestellt ist, wird jeweils auf die Zelle (i)u und (i+1)b
aufgeschlagen. Nach der Aufsummierung der Wellensprünge wird der geteilten
Zelle (i) durch konservative Mittelung
ein neuer Mittelwert
wird auf alle
teilweise oder ganz überstrichenen Zellen verteilt. Der Sprung der Flamme, wie
sie in Abbildung
7-11 dargestellt ist, wird jeweils auf die Zelle (i)u und (i+1)b
aufgeschlagen. Nach der Aufsummierung der Wellensprünge wird der geteilten
Zelle (i) durch konservative Mittelung
ein neuer Mittelwert
Gleichung 7-48: 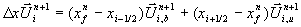
zugeordnet und die Teilzellen (i)u,b eliminiert, während die Teilzellen (i+1)u,b gespeichert werden.
Durch diese Vorgehensweise wird das Problem der CFL-Bedingung für kleine Zellen
umgangen.
Dieses Verfahren ist sehr robust und wird im folgenden als
Referenzverfahren für die Simulation von Flammen und DDT in einer Dimension
benutzt. Die Nachteile dieses Verfahrens sind, daß es beim Übergang auf zwei
Dimensionen sehr aufwendig wird und die propagierten Teilstücke der alten Front
keine geschlossene neue Front ergeben. Diese muß durch Interpolation erzeugt
werden. Hier wird ein neues Verfahren vorgestellt, daß dieses Problem umgeht
und wesentlich einfacher zu realisieren ist.
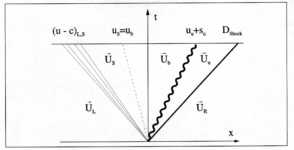
Abbildung 7-10: Flammen-Riemann-Problem
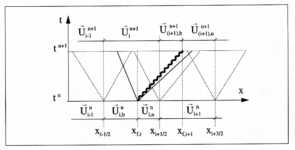
Abbildung 7-11:
Flammen-Tracking in 1-D
Flammen-Rekonstruktionsverfahren
Wellen- und Flußformulierung
Das Flammen-Rekonstruktionsverfahren versucht, das im
vorigen Abschnitt beschriebene numerische Verfahren soweit wie möglich zu
vereinfachen und dabei die Vorteile des Tracking beizubehalten. Die Grundidee
ist es, nur noch die Flamme als Diskontinuität zu betrachten und die
Speicherung der Zustände in den verbrannten und unverbrannten Teilzellen zu
umgehen.
Das Verfahren soll folgende Eigenschaften besitzen:
·
Das Verfahren soll konservativ und zu allen
Standard-Capturing-Verfahren kompatibel sein, die in der konservativen
Flußformulierung mit einem zusätzlichen Quellterm geschrieben sind. Die
Formulierung soll vereinbar sein mit dem Richtungs-Operator-Splitting. Das
Verfahren soll dadurch über einfache Schnittstellen in andere Codes implementiert
werden können.
·
Die aufwendige Speicherung der komplizierten
Teilgeometrien der Mischzellen und die komplizierte Bilanzierung für diese
Geometrien, die bei reinen Tracking-Verfahren auftreten, sollen dadurch
vermieden werden, daß die Bilanzgleichungen nur für Zellmittelwerte auf einem
kartesischen Gitter konstanter Schrittweite gelöst werden. Dies wird möglich
durch die korrekte Auswertung der Zustandsgrößen an den Zellflächen aufgrund
einer Rekonstruktion von unverbrannten und verbrannten Zuständen über der
Flamme.
·
Die Rekonstruktion basiert auf der Erhaltung der
konservativen Größen und den Rankine-Hugoniot-Sprungbedingungen über der
Flamme, wodurch die Kopplung zwischen der wärmefreisetzenden Flamme und der
Strömung in korrekter, nichttrivialer Weise gewährleistet werden soll.
Aufbauend auf den numerischen Fluß des Roe-Verfahrens (Gleichung 7-35,
Gleichung 7-42)
wird die einfache Wellenform (Gleichung
7-42) um den Flammenanteil 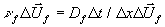 zu
zu
Gleichung 7-49: 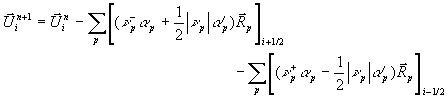
erweitert. Hierbei muß der Flammensprung  derart beschaffen
sein, daß die gasdynamischen Effekte der Flamme berücksichtigt werden. Das
Verfahren sei zunächst in einer Dimension anhand der Abbildung 7-12 erklärt. Die Zelle (i) sei die Mischzelle zum Zeitpunkt tn. Aus der Flammenposition
derart beschaffen
sein, daß die gasdynamischen Effekte der Flamme berücksichtigt werden. Das
Verfahren sei zunächst in einer Dimension anhand der Abbildung 7-12 erklärt. Die Zelle (i) sei die Mischzelle zum Zeitpunkt tn. Aus der Flammenposition  läßt sich der Anteil
von verbranntem und unverbranntem Volumen Vb
und Vu ermitteln und der
Volumenanteil
läßt sich der Anteil
von verbranntem und unverbranntem Volumen Vb
und Vu ermitteln und der
Volumenanteil  des verbrannten Gases
der Mischzelle
des verbrannten Gases
der Mischzelle
Gleichung 7-50: 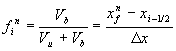
angeben. Ausgangspunkt der Rekonstruktion ist der Mittelwert
der Zustandsgrößen in der Mischzelle 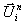 . Mit den verbrannten
. Mit den verbrannten 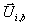 und unverbrannten
Zuständen
und unverbrannten
Zuständen 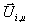 , die als Funktion des verbrannten Volumenanteils
spezifiziert werden müssen, werden nun die Roe-Riemann-Probleme an der Zellfläche
xi-1/2 mit
, die als Funktion des verbrannten Volumenanteils
spezifiziert werden müssen, werden nun die Roe-Riemann-Probleme an der Zellfläche
xi-1/2 mit 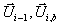 und an der Zellfläche
xi+1/2 mit
und an der Zellfläche
xi+1/2 mit 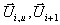 gelöst. Dies würde
einer numerischen Flußauswertung in erster Ordnung
gelöst. Dies würde
einer numerischen Flußauswertung in erster Ordnung
Gleichung 7-51: 
entsprechen. Aus der Lösung der Roe-Riemann-Probleme folgen
nun die einzelnen Wellensprünge an den Zellflächen
Gleichung 7-52: 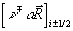 ,
,
wobei die rechtslaufende bzw. linkslaufende Welle aus der
Zellfläche xi-1/2 bzw. xi+1/2 ein Teilvolumen 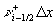 bzw.
bzw. 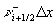 der Zelle (i) überstreicht (der Index p der p-ten
Welle wurde zunächst weggelassen).
der Zelle (i) überstreicht (der Index p der p-ten
Welle wurde zunächst weggelassen).
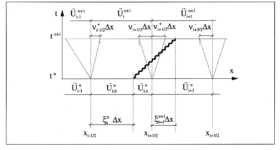
Abbildung 7-12:
Wellenverteilung beim Flammen-Rekonstruktionsverfahren
Bezüglich der Terme höherer Ordnung a' muß beachtet werden, daß
keine Informationen von der anderen Flammenseite benutzt werden, damit nicht
über die Flammendiskontinuität hinweg diskretisiert wird. Steigungen in der
Mischzelle si
werden entweder zu Null gesetzt oder aus der jeweiligen Richtung extrapoliert
Gleichung 7-53:  .
.
Das Verfahren ist daher an der Diskontinuität erster Ordnung
genau.
Zusätzlich zu den gasdynamischen Wellensprüngen 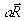 muß der Sprung der
Flamme
muß der Sprung der
Flamme 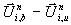 auf das Volumen Df Dt verteilt werden. Hier
wird Df aus dem
unverbrannten Zustand
auf das Volumen Df Dt verteilt werden. Hier
wird Df aus dem
unverbrannten Zustand 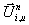 berechnet zu
berechnet zu
Gleichung 7-54: 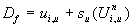 .
.
Für Df
> 0 bleibt die Flamme während des Zeitschritts Dt entweder in der Zelle (i) oder wandert in die Zelle (i+1) und die neuen verbrannten Volumenanteile
berechnen sich zu
Gleichung 7-55: 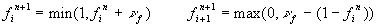 .
.
Die Bilanz für die Zellen j = i und j = i + 1
schreibt sich in Anlehnung an Abbildung
7-12 mit 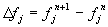
Gleichung 7-56: 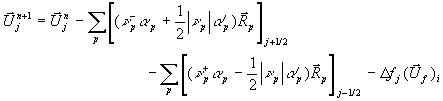
Hier wird der Flammensprung 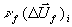 aus Zelle (i) also auf zwei Nachbarzellen verteilt
und so wie beim Flammen-Tracking die Problematik der CFL-Bedingung für kleine
Teilzellen f Dx bzw. (1-f) Dx umgangen. Der große Vorteil
dieser Darstellung ist, daß die Bilanzgleichungen nur für Zellmittelwerte
aus Zelle (i) also auf zwei Nachbarzellen verteilt
und so wie beim Flammen-Tracking die Problematik der CFL-Bedingung für kleine
Teilzellen f Dx bzw. (1-f) Dx umgangen. Der große Vorteil
dieser Darstellung ist, daß die Bilanzgleichungen nur für Zellmittelwerte 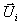 berechnet werden.
Somit werden die aufwendige Speicherung und die Bilanzierung der Teilzellen,
wie sie beim Flammen-Tracking auftreten, überflüssig.
berechnet werden.
Somit werden die aufwendige Speicherung und die Bilanzierung der Teilzellen,
wie sie beim Flammen-Tracking auftreten, überflüssig.
Eine andere Darstellungsweise geht von der Flußformulierung
aus und beachtet, daß die Flamme durch ihre Relativbewegung zur Strömung eine
chemische Wärmefreisetzung verursacht, die als Quellterm in der Speziesgleichung
wiederzufinden ist. Dabei sei die Wellenformulierung für eine einzelne
stationäre Flamme, die den unverbrannten Zustand 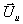 vom verbrannten
Zustand
vom verbrannten
Zustand 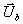 trennt und sich mit
konstanter Geschwindigkeit Df
innerhalb einer Zelle (i) fortbewegt,
ausgedrückt. Demnach verschwinden sämtliche gasdynamischen Wellen aus der
Bilanz und nur noch der Flammensprung trägt zur Änderung des Zustandsvektors
bei
trennt und sich mit
konstanter Geschwindigkeit Df
innerhalb einer Zelle (i) fortbewegt,
ausgedrückt. Demnach verschwinden sämtliche gasdynamischen Wellen aus der
Bilanz und nur noch der Flammensprung trägt zur Änderung des Zustandsvektors
bei
Gleichung 7-57: 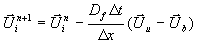 .
.
Über die Sprungbedingungen für Masse, Impuls und Energie
Gleichung 7-58: 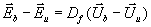
kann der Wellensprung in eine Flußdifferenz umgeformt
werden. Die numerischen Flüsse an den Zellgrenzen entsprechen dann jeweils den
Flüssen im Verbrannten bzw. Unverbrannten. Für die Speziesgleichung muß die Relativbewegung
berücksichtigt werden. Der Speziessprung schreibt sich dann mit Df = uu + su
= ub + sb zu
Gleichung 7-59: 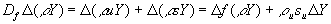 .
.
Die Bilanz nimmt dann die Erhaltungsform mit zusätzlichem
Quellterm 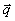 in der Speziesgleichung
in der Speziesgleichung
Gleichung 7-60: 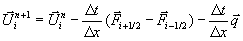
mit
Gleichung 7-61: 
an.
Diese Formulierung in Erhaltungsform mit zusätzlichem Quellterm
ist in vielen Anwendungen wiederzufinden und zeigt, daß das Verfahren
kompatibel ist mit sämtlichen Strömungslösern, die auf Flußbilanzen und
zusätzlichen Quelltermen beruhen.
Für den Fall, daß die Flamme über die Zellgrenze xi+1/2 läuft, muß der numerische
Fluß aufgrund des erfahrenen Wellensprungs in einer korrekten, zeitlich
gemittelten Form modifiziert werden
Gleichung 7-62: 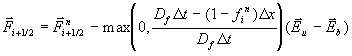 .
.
Analog zu dieser zeitlichen Mittelung muß der Quellterm auf
die Zellen (i) und (i+1) verteilt werden. Die verbrannten
Volumenanteile ändern sich in beiden Zellen durch die Flamme um jeweils 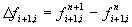 . Anteilmäßig wird der Quellterm
. Anteilmäßig wird der Quellterm 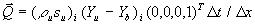 auf die Zellen (i) und (i+1) verteilt. Die Quellterme in den Speziesgleichungen lauten
dann
auf die Zellen (i) und (i+1) verteilt. Die Quellterme in den Speziesgleichungen lauten
dann
Gleichung 7-63: 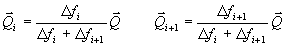 .
.
Beim Übergang auf zwei Dimensionen muß noch die räumliche
Mittelung über einer Zellfläche beachtet werden. Dies wird allerdings nicht
mehr erläutert, da hier durchweg die Wellendarstellung benutzt wurde.
Rekonstruktion der verbrannten und
unverbrannten Zustände
Zur Vervollständigung der Lösung müssen noch die Zustände 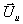 und
und 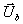 aus dem bekannten
Zellmittelwert der Mischzelle
aus dem bekannten
Zellmittelwert der Mischzelle 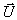 bestimmt werden. Aufgrund
der Erhaltung der konservativen Größen muß sich der Mittelwert aus einer
Volumengewichtung des verbrannten und unverbrannten Zustandes ergeben
bestimmt werden. Aufgrund
der Erhaltung der konservativen Größen muß sich der Mittelwert aus einer
Volumengewichtung des verbrannten und unverbrannten Zustandes ergeben
Gleichung 7-64: 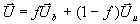 ,
,
wobei f der
bekannte Volumenanteil des verbrannten Gases ist. Der eindimensionale Fall
liefert vier Gleichungen für die acht unbekannten Größen (r,u,p,Y)u und (r,u,p,Y)b
Gleichung 7-65: 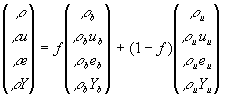
mit der einfachen Energieformel 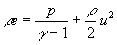 . Aus den Annahmen einer stationären Flamme folgt die konstante
Ausbreitungsgeschwindigkeit Df
der Flamme
. Aus den Annahmen einer stationären Flamme folgt die konstante
Ausbreitungsgeschwindigkeit Df
der Flamme
Gleichung 7-66: 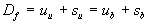 .
.
Schließlich liefern die Rankine-Hugoniot-Bedingungen für
Masse, Impuls und Energie über der Flamme 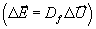 den konstanten
Massenfluß rs
durch die Flamme
den konstanten
Massenfluß rs
durch die Flamme
Gleichung 7-67: 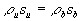
die Rayleigh-Gerade mit P
= pb/pu und V =
ru/rb
Gleichung 7-68: 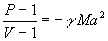
und die Volumenbeziehung
Gleichung 7-69: 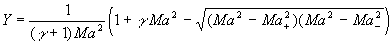
mit den Definitionen
Gleichung 7-70: 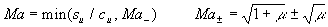
Gleichung 7-71: 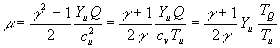 .
.
Die Abfrage nach dem Minimum in der Mach-Zahl sichert, daß
die Flamme nicht schneller werden kann als die zugehörige CJ-Flamme. Neben den vier weiteren Gleichungen sind su und sb als neue unbekannte Größen hinzugekommen. Zur Lösung
des Systems werden noch zwei weitere Informationen geliefert. Aus der
kompletten Verbrennung folgt der Massenbruch im Verbrannten zu
Gleichung 7-72: 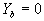
und das vorgegebene Brenngesetz lautet
Gleichung 7-73: 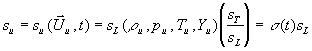 ,
,
wobei s(t) die zeitabhängige, dimensionslose
Flammenoberfläche darstellt. Damit ist das System geschlossen und kann
iterativ, z.B. mittels einer Fixpunktiteration oder dem Newton-Verfahren,
gelöst werden. Zusätzliche Beschränkungen, die eingehalten werden, resultieren
aus der Positivität des Massenbruches
Gleichung 7-74: 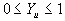
und der minimalen isobaren Vmin bzw. maximal möglichen Volumenausdehnung im CJ-Zustand Vmax
Gleichung 7-75: 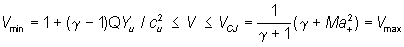 .
.
Erweiterung auf zwei Dimensionen
Die Erweiterung auf zwei Dimensionen erfolgt im
Operator-Splitting. So wird hier lediglich die Behandlung in x-Richtung erläutert. Während im eindimensionalen
Fall der verbrannte Volumenanteil durch die Flammenposition direkt berechenbar
ist, wird in zwei Dimensionen die Flammengeometrie benötigt, um fi,j zu berechnen. Hierzu
wird das skalare G-Feld auf den
Zellecken der Zelle (i,j) definiert  . Die Flamme wird identifiziert als die Höhenlinie G = G0 und wird innerhalb der
Zelle als stückweise lineare Verteilung approximiert. Die Flamme schneidet die
Oberflächen der Zelle und definiert somit den Flächenanteil h
des verbrannten Gases. In Abbildung
7-13 sind den vier Zellflächen der Zelle (i,j), die das Intervall [xi-1/2,xi+1/2]
x [yj-1/2,yj+1/2]
definiert, vier verbrannte Zellflächenanteile h1 bis h4
zugeordnet, die aus der Verteilung von G
bestimmt werden. Aus den Werten h1,...,4 berechnet sich der verbrannte
Volumenanteil fi,j , zum
Beispiel fi,j = 1/2 (h1
+ h3).
Aus der G-Verteilung folgt weiterhin
der Normalenvektor
. Die Flamme wird identifiziert als die Höhenlinie G = G0 und wird innerhalb der
Zelle als stückweise lineare Verteilung approximiert. Die Flamme schneidet die
Oberflächen der Zelle und definiert somit den Flächenanteil h
des verbrannten Gases. In Abbildung
7-13 sind den vier Zellflächen der Zelle (i,j), die das Intervall [xi-1/2,xi+1/2]
x [yj-1/2,yj+1/2]
definiert, vier verbrannte Zellflächenanteile h1 bis h4
zugeordnet, die aus der Verteilung von G
bestimmt werden. Aus den Werten h1,...,4 berechnet sich der verbrannte
Volumenanteil fi,j , zum
Beispiel fi,j = 1/2 (h1
+ h3).
Aus der G-Verteilung folgt weiterhin
der Normalenvektor 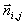 (Indizes werden der
Einfachheit halber weggelassen), der durch
(Indizes werden der
Einfachheit halber weggelassen), der durch 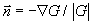 bzw.
bzw. 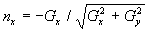 und
und 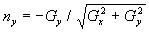 definiert ist. Die partiellen
Ableitungen von G werden als
Mittelwerte der Differenzenquotienten auf sich gegenüberliegenden Zellflächen
approximiert
definiert ist. Die partiellen
Ableitungen von G werden als
Mittelwerte der Differenzenquotienten auf sich gegenüberliegenden Zellflächen
approximiert
Gleichung 7-76: 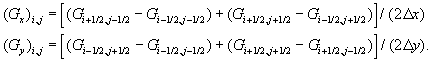
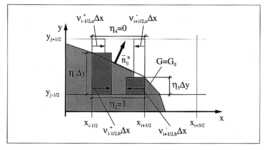
Abbildung 7-13:
Verteilung der gasdynamischen Wellen in zwei Dimensionen im
x-Operator-Splitting
Rekonstruktion
Zusätzlich zu Gleichung
7-65 muß die Impulserhaltung in y-Richtung
Gleichung 7-77: 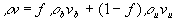
gelöst werden. Die Rekonstruktion der verbrannten und
unverbrannten Zustände erfolgt nun normal zur Flamme. Dazu werden die
Geschwindigkeiten u und v in die Geschwindigkeiten normal 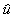 und tangential
und tangential 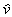 zur Flamme aufgespalten
zur Flamme aufgespalten
Gleichung 7-78: 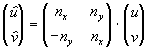 .
.
Transformiert auf die Normalen- und Tangentialrichtung
ändern sich die Erhaltungsgleichungen zu
Gleichung 7-79: 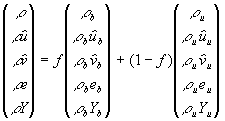
mit der einfachen Energieformel
Gleichung 7-80: 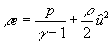 .
.
Das bedeutet, daß eine weitere Gleichung und zwei neue
Unbekannte hinzukommen. Die fehlende Information wird durch die Forderung nach
konstanten Tangentialgeschwindigkeiten über der Flamme
Gleichung 7-81: 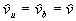
geliefert. Die Rankine-Hugoniot-Sprungbedingungen bleiben
dagegen unverändert und bestehen weiterhin aus Gleichung 7-67, Gleichung 7-68
und Gleichung 7-69.
Mit den restlichen Vorgaben Yb
= 0 und dem Brenngesetz wird dieses System gelöst und die Normal- und
Tangentialgeschwindigkeit zurück auf die x,y-Richtungen
transformiert
Gleichung 7-82: 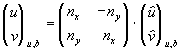 .
.
Wellenverteilung
Nach der Rekonstruktion der verbrannten und unverbrannten
Zustände in sämtlichen Mischzellen werden z.B. für die Zellfläche (i+1/2,,j), die in einen verbrannten, hi+1/2,j
Dy
großen Anteil (h3 Dy in Abbildung
7-13) und einen unverbrannten, (1-hi+1/2,j)
Dy
großen Anteil unterteilt ist, die Roe-Riemann-Probleme im Verbrannten und
Unverbrannten gelöst
Gleichung 7-83: 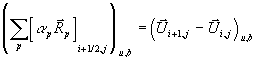 .
.
Die Wellenbeiträge der Zellfläche sind dann ein
flächengewichteter Mittelwert der verbrannten und der unverbrannten
Wellenbeiträge
Gleichung 7-84: 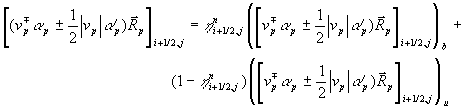
Hier wird h zum Zeitpunkt tn ausgewertet. Dies ist kompatibel mit der ersten
Genauigkeitsordnung an der Flamme durch die Limitierung beim Überschreiten
derselben.
Mit den rekonstruierten Geschwindigkeiten kann der
Flammenfortschritt mit der Flammenausbreitungsgeschwindigkeit 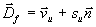 (in x-Richtung Dx = uu + sunx) durch
Lösung der G-Gleichung berechnet
werden. Bei der Verteilung des Flammensprungs liegt das G-Feld zum neuen Zeitpunkt Gn+1
vor. Im allgemeinen Fall tragen zur Änderung der Zustandsgrößen neben dem
Flammenstück in der betrachteten Zelle auch die über die Zellflächen propagierten
Flammenstücke der Nachbarzellen
(in x-Richtung Dx = uu + sunx) durch
Lösung der G-Gleichung berechnet
werden. Bei der Verteilung des Flammensprungs liegt das G-Feld zum neuen Zeitpunkt Gn+1
vor. Im allgemeinen Fall tragen zur Änderung der Zustandsgrößen neben dem
Flammenstück in der betrachteten Zelle auch die über die Zellflächen propagierten
Flammenstücke der Nachbarzellen 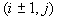 bei. Die Änderung des
verbrannten Volumenanteils
bei. Die Änderung des
verbrannten Volumenanteils 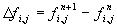 setzt sich im
allgemeinen aus dem zentralen Anteil
setzt sich im
allgemeinen aus dem zentralen Anteil 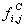 des
Flammenfortschritts innerhalb der Zelle und den Anteilen des
Flammenfortschritts
des
Flammenfortschritts innerhalb der Zelle und den Anteilen des
Flammenfortschritts 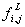 über der Zellfläche (i-1/2,j) und
über der Zellfläche (i-1/2,j) und 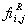 über der Zellfläche (i+1/2,j) zusammen
über der Zellfläche (i+1/2,j) zusammen
Gleichung 7-85: 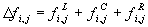 .
.
Die Ermittlung der Teilvolumina 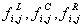 ist in Abbildung 7-14
durch unterschiedliche Schattierungen angedeutet und resultiert aus
geometrischen Zusammenhängen. Für das Beispiel in Abbildung 7-14 resultieren die
Anteile aus den Flächenanteilen (siehe Abbildung
7-14) zum alten und neuen Zeitpunkt zu
ist in Abbildung 7-14
durch unterschiedliche Schattierungen angedeutet und resultiert aus
geometrischen Zusammenhängen. Für das Beispiel in Abbildung 7-14 resultieren die
Anteile aus den Flächenanteilen (siehe Abbildung
7-14) zum alten und neuen Zeitpunkt zu
Gleichung 7-86: 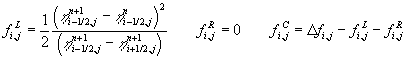 .
.
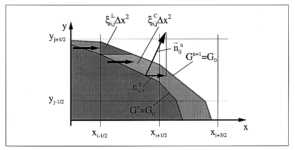
Abbildung 7-14:
Wellenverteilung der Flamme in zwei Dimensionen im x-Operator-Splitting
Die gesamte Zustandsänderung aufgrund des Flammenfortschritts
ergibt sich dann aus den Flammensprüngen der Zellen (i-1,j), (i,j) und (i+1,j)
zu
Gleichung 7-87: 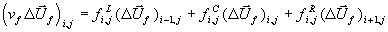 .
.
Im folgenden wird die numerische Lösung der G-Gleichung vorgestellt, die zur
Bestimmung der Lage der Flammenfront im numerischen Gitter herangezogen wird.
Numerische Lösung der skalaren
Feldgleichung
Eigenschaften der skalaren
Feldgleichung
Die Erfassung des Flammenfortschritts erfolgt durch
Berechnung eines Skalars G auf dem
numerischen Gitter.
Der explizite Flammenfortschritt aufgrund des
Flammentransportes durch die Strömung und aufgrund der Flammenausbreitung
relativ zur Strömung wird durch die Advektionsgleichung
Gleichung 7-88: 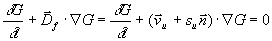
beschrieben, in der die Größe 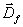 die absolute
Flammenausbreitungsgeschwindigkeit
die absolute
Flammenausbreitungsgeschwindigkeit 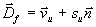 darstellt.
darstellt.
Sie gilt zunächst nur für die Flammenfläche G = G0. Williams [62]
interpretiert die G-Gleichung (Gleichung 7-88)
als geeignete Darstellung für den Flammenskalar 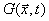 im ganzen
Strömungsfeld. Dieser Ansatz erfordert jedoch, daß fern der Flamme geeignete
sinnvolle Werte der Brenngeschwindigkeit su
im unverbrannten und sb im
verbrannten Gas definiert werden können. Dies ist im allgemeinen jedoch nicht
der Fall, da alle anderen Isoflächen
im ganzen
Strömungsfeld. Dieser Ansatz erfordert jedoch, daß fern der Flamme geeignete
sinnvolle Werte der Brenngeschwindigkeit su
im unverbrannten und sb im
verbrannten Gas definiert werden können. Dies ist im allgemeinen jedoch nicht
der Fall, da alle anderen Isoflächen  in keiner Weise an
das Strömungsfeld koppeln. Daher besteht ein Freiheitgrad in der Wahl einer
numerisch vorteilhaften Struktur von G
fern der Flamme G = G0.
in keiner Weise an
das Strömungsfeld koppeln. Daher besteht ein Freiheitgrad in der Wahl einer
numerisch vorteilhaften Struktur von G
fern der Flamme G = G0.
Für das Flammen-Rekonstruktionsverfahren notwendig ist
lediglich, daß die Verteilung des Skalars G
stets glatt ist, um Interpolationfehler durch große Gradienten bei der
Ermittlung der Flammenposition auszuschließen. Ideen zur Erfüllung dieser
Forderung an das skalare Feld findet man bei Sussman et. al (1994) [63]. Bei der Entwicklung von „level
set"-Verfahren zur numerischen Behandlung von Kontaktunstetigkeiten (wie
z.B. Gasblasen in Flüssigkeiten) wird das skalare Feld entsprechend der
Transportgeschwindigkeit durch die Strömung verformt. Der Forderung nach einer
glatten Verteilung von G wird dadurch
nachgekommen, daß 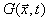 als Abstandsfunktion
von G0 definiert wird und
zu jeder Zeit die zweite zu lösende Gleichung
als Abstandsfunktion
von G0 definiert wird und
zu jeder Zeit die zweite zu lösende Gleichung
Gleichung 7-89: 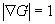
die G-Verteilung
für 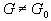 definiert. Diese
Gleichung besagt, daß der Normalenabstand dxn
zweier Isoflächen G und G + dG gleich ist der Differenz der G-Werte dG, wie bereits oben beschrieben wurde.
definiert. Diese
Gleichung besagt, daß der Normalenabstand dxn
zweier Isoflächen G und G + dG gleich ist der Differenz der G-Werte dG, wie bereits oben beschrieben wurde.
Die numerische Kombination der beiden Gleichungen (G-Gleichung und Abstandsfunktion)
erfordert einen endlichen Übergangsbereich. Obwohl die G-Gleichung nur an der Flammenfläche G = G0 definiert ist, wird sie nahe der Flamme in einem
endlichen Bereich um G = G0
gelöst. Durch diese Vorgabe ist es möglich, für die Lösung der G-Gleichung effiziente Standardverfahren,
die in Anlehnung an stoßauflösende Verfahren entwickelt wurden, anzuwenden.
Diese Verfahren auf der Basis von level sets garantieren den korrekten
Transport der Isoflächen, ohne die genaue Position von G = G0 zu ermitteln und einzelne Punkte der Front direkt
zu verfolgen, was einem Tracking-Verfahren gleich käme. In einem zweiten
Schritt wird die Gleichung der Abstandsfunktion außerhalb des endlichen
Bereichs gelöst.
Lösung der G-Gleichung
Die Besonderheit der G-Gleichung
ist, daß sie die Form der Hamilton-Jacobi-Gleichung besitzt. Darauf bauen Lösungsansätze
auf, die in den Veröffentlichungen von Osher und Sethian [52],[53] nachgelesen werden
können. In diesen Arbeiten werden bekannte, stoßauflösende Verfahren zur Lösung
herangezogen.
Hier soll jedoch von der bereits bekannten hyperbolischen
nicht-konservativen Form
Gleichung 7-90: 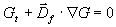
ausgegangen werden. Diese wird im
Richtungs-Operator-Splitting mit der entsprechenden Komponente der Flammenausbreitungsgeschwindigkeit
D = uu + snx
bzw. D = vu+sny
für die x- bzw. y-Richtung gelöst:
Gleichung 7-91: 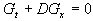 .
.
Hier sind nx,ny
die Komponenten des Normalenvektors in den jeweiligen Richtungen. Die
Diskretisierung erfolgt auf den Ecken der Zellen, an denen die G-Werte definiert sind. Hierzu müssen
geeignete Werte der Geschwindigkeiten D,
die nur im rekonstruierten Zellzentrum definiert sind, den Zellecken zugeordnet
werden. Zur Lösung wird ein einfaches Diskretisierungsschema erster Ordnung,
welches das Vorzeichen der Transportgeschwindigkeit berücksichtigt („upwind“),
benutzt. Zur Vereinfachung sind nur die Indizes für die x-Richtung dargestellt:
Gleichung 7-92: 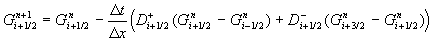 .
.
Der Transport von Gradienten von G erfolgt entsprechend dem Vorzeichen der Geschwindigkeit D mit der Definition
Gleichung 7-93:  .
.
Die Zuordnung der Geschwindigkeiten von den rekonstruierten
Werten im Zellzentrum Di,j
auf die Zellecken Di+1/2,j+1/2
erfolgt entsprechend dem geringsten Abstand eines Flammensegments zur
jeweiligen Zellecke. Eine Zellecke (i+1/2,j+1/2)
ist in Abbildung
7-15 durch ausgefüllte Kreise gekennzeichnet und kann von maximal vier
Mischzellen (i,j),(i+1,j),(i,j+1),(i+1,j+1),
in denen jeweils eine Flamme mit der Flammengeschwindigkeit Di,j, Di+1,j, Di,j+1,
Di+1,j+1 rekonstruiert würde, umgeben sein, die ihre
Ausbreitungsgeschwindigkeit bestimmen. Eine einfache, sinnvolle Wahl, die
vorgenommen wurde, setzt Di+1/2,
j+1/2 gleich der Flammengeschwindigkeit in der Zelle mit dem
kürzesten Abstand der Flamme zur betrachteten Zellecke. Liegt die Zellecke z.B.
im Verbrannten bzw. Unverbrannten, so ist der Volumenanteil des Verbrannten f bzw. des Unverbrannten 1-f ein Maß für den Abstand (siehe Abbildung 7-15).

Abbildung 7-15:
Expliziter Flammentransport mit Zuordnung der Geschwindigkeiten an den
Zellecken und Berücksichtigung des Überschreitens der Flamme über Zellecken
Gleichung 7-94: 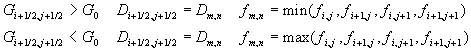
Die komplette Darstellung der Flammenfront innerhalb einer
Zelle (i,j) durch Interpolation der G-Werte erfordert mindestens drei
Zelleckenwerte. Beim Übergang eines Flammensegmentes über eine Zellecke kann
aus einer ursprünglich verbrannten bzw. unverbrannten Zelle eine Mischzelle
werden. In Abbildung
7-15 sind dies die Zellen (i-1,j-1)
und (i-1,j), die im neuen Zeitschritt
Mischzellen sind. Den Zellecken (i-3/2,j-3/2),
(i-3/2,j-1/2) und (i-3/2,j+1/2), die in Abbildung 7-15
durch nicht ausgefüllte Kreise gekennzeichnet sind, werden die
Geschwindigkeitswerte der Nachbarn, die von der Flamme überstrichen werden, zugeordnet
Gleichung 7-95: 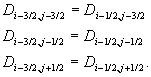
Damit sind die notwendigen Informationen bereitgestellt.
Diese Formulierung ist nur von erster Genauigkeitsordnung, da die
Geschwindigkeiten nur bei der Flamme selbst definiert sind, was bei den
Arbeiten von Osher und Sethian stets duch die Vorgabe einer Ausbreitungsgeschwindigkeit
umgangen wird. Somit können dort Verfahren höherer Ordnung direkt übertragen
werden. In diesem Fall jedoch würde eine Erweiterung auf zweite Ordnung das Einbeziehen
von Querableitungen tangential zur Flamme erfordern. Zusätzlich würde eine
zweite Flammenrekonstruktion nötig, um auch zeitlich auf die zweite
Genauigkeitsordnung zu kommen. Trotz der ersten Genauigkeitsordnung können die
grundlegenden Eigenschaften des Rekonstruktionsverfahrens bereits deutlich gemacht
werden.
Lösung der Abstandsfunktion
Die Abstandsfunktionsgleichung
Gleichung 7-96: 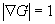
bewirkt, daß G-G0
gleich dem normalen Abstand des Punktes mit dem Wert G von der Isofläche G0
ist, und wird für Punkte außerhalb der Flammenzone gelöst. Die Flammenzone
erstreckt sich jeweils eine Zellenweite ins Unverbrannte und Verbrannte und
beinhaltet noch die Zellecken, die durch den Übergang der Flamme in eine
unverbrannte oder verbrannte Zelle zu Zellecken einer neuen Mischzelle werden.
Für die restlichen Zellecken werden die G-Werte
entsprechend ihres normalen Abstands von G
= G0 geglättet.
Sussman et al. [63]
lösen zunächst die G-Gleichung mit der
Strömungsgeschwindigkeit, die im ganzen Feld wohldefiniert ist, und lösen im
Anschluß die Gleichung für die Abstandsfunktion ebenfalls für das gesamte Feld.
Danach soll die Position 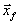 der Fläche G = G0 durch die
Reinitialisierung unbeeinträchtigt bleiben. Dies kann theoretisch gezeigt
werden. Numerisch allerdings kann die Beibehaltung der korrekten
Flammenposition nicht garantiert werden (siehe Sussman et al. [64]).
Somit werden nur die Punkte außerhalb der Flammenzone, wobei die Punkte
innerhalb der Flammenzone als Randbedingung benutzt werden, berechnet. Die
Differentialgleichung
der Fläche G = G0 durch die
Reinitialisierung unbeeinträchtigt bleiben. Dies kann theoretisch gezeigt
werden. Numerisch allerdings kann die Beibehaltung der korrekten
Flammenposition nicht garantiert werden (siehe Sussman et al. [64]).
Somit werden nur die Punkte außerhalb der Flammenzone, wobei die Punkte
innerhalb der Flammenzone als Randbedingung benutzt werden, berechnet. Die
Differentialgleichung
Gleichung 7-97: 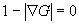
wird aus praktischen Gründen modifiziert zu
Gleichung 7-98: 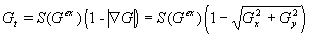
und wird iterativ in zwei Dimensionen bis zum stationären
Zustand Gt = 0 gelöst.
Hier bedeutet Gex
die G-Verteilung nach der Lösung des
expliziten Transports, wie er im vorigen Kapitel beschrieben wurde. In dieser
Verteilung sind lediglich die Punkte innerhalb der Flammenzone verändert. Die
Position der Flamme Gex = G0
ist ausschlaggebend für die Funktion S(Gex),
die das Vorzeichen von Gex
wiedergibt. Zu numerischen Zwecken wird diese Vorzeichenfunktion mit einem
kleinen numerischen Wert e durch den Ansatz
Gleichung 7-99: 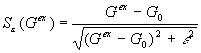
modifiziert, wodurch Störungen von 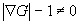 stets in Richtung
stets in Richtung 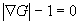 zurückgeglättet
werden. Schreibt man die Iterationsgleichung (Gleichung
7-98) um zu
zurückgeglättet
werden. Schreibt man die Iterationsgleichung (Gleichung
7-98) um zu
Gleichung 7-100: 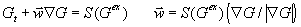 ,
,
so erkennt man die nichtlineare hyperbolische Gleichung mit
den durch den Vektor 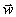 gegebenen
Charakteristiken. Der Vektor
gegebenen
Charakteristiken. Der Vektor 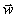 ist ein Normalenvektor,
der stets weg von G = G0
zeigt. Informationen breiten sich stets von der Flamme mit der Geschwindigkeit
ist ein Normalenvektor,
der stets weg von G = G0
zeigt. Informationen breiten sich stets von der Flamme mit der Geschwindigkeit 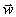 aus.
aus.
Weitere Informationen zur Diskretisierung der Gleichung 7-98
finden sich bei [13].
Die neu berechnete G-Verteilung
stimmt an der Flamme mit der expliziten überein Gn+1 = Gex und fern der Flamme konvergiert G aufgrund von Gt = 0 zu 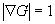 und somit zum
tatsächlichen Abstand.
und somit zum
tatsächlichen Abstand.
7.5 Zusammenfassung
Das Kapitel gibt zunächst einen Überblick über die
wesentlichen Elemente von numerischen Lösungsverfahren. Die grundlegenden
Erhaltungsgleichungen werden vorgestellt und ihre Diskretisierung kurz
diskutiert. Im SFB 224 wurden sowohl kommerzielle Programmpakete eingesetzt,
wie auch Rechenprogramme selbst entwickelt. Erstere dienten als Ausgangspunkt
für die Implementierung verbesserter Modelle für die Simulation des Wärmeübergangs
im Zylinder oder die Berechnung der Strahlausbreitung, der Zerstäubung und der
Verdampfung von Kraftstoff oder der Zündung, Verbrennung und Schadstoffbildung
in Dieselmotoren. Die in den kommerziellen Programmen implementierten
Lösungsverfahren stellen als Grundlage solcher Arbeiten einen geeigneten
Ausgangspunkt dar. Detaillierte Untersuchungen der kalten Strömung in den
Einlaßkanälen und der Ventilumströmung im Motor sowie der Wirbeldynamik bis zum
Ende des Kompressionstaktes wurden dagegen mit vollständig eigenentwickelter
Software durchgeführt. Besondere numerische Anforderungen an das
Lösungsverfahren bereitetauch die Berechnung der Ausbreitung vorgemischter
Flammen. Da die sehr dünnen Flammenstrukturen mit vertretbarem Aufwand numerisch
nicht aufgelöst werden können, sind zwei neue numerische Verfahren entwickelt
worden, bei denen die Flamme als Diskontinuität im Strömungsfeld aufgefaßt
wird. Der Beschreibung dieser Verfahren ist der größte Teil dieses Kapitel
gewidmet.
7.6 Abbildungsverzeichnis
Abbildung
7-1: Diskretisierung der 1-D Eulergleichungen in Raum und Zeit
Abbildung 7-2: Zentrale und upwind Diskretisierung
Abbildung 7-3: Flußberechnung beim Verfahren von Godunov und
von Roe
Abbildung 7-4: Positionen der Geschwindigkeitsvektoren (links),
Prinzip des Konvektionsalgorithmus (rechts)
Abbildung 7-5: Testrechnungen für Konvektionsalgorithmen
Abbildung 7-6: Prinzip des Ausbreitungsalgorithmus
Abbildung 7-7: Testrechnung für Ausbreitungsalgorithmen
Abbildung 7-8: Schematische Darstellung eines Volumenelementes
aus dem Entrainment-Modell
Abbildung 7-9: Schematische Darstellung der Positionierung und
der Verteilung der Quellterme
Abbildung 7-10: Flammen-Riemann-Problem
Abbildung 7-11: Flammen-Tracking in 1-D
Abbildung 7-12: Wellenverteilung beim
Flammen-Rekonstruktionsverfahren
Abbildung 7-13: Verteilung der gasdynamischen Wellen in zwei
Dimensionen im x-Operator-Splitting
Abbildung 7-14: Wellenverteilung der Flamme in zwei Dimensionen
im x-Operator-Splitting
Abbildung 7-15: Expliziter Flammentransport mit Zuordnung der
Geschwindigkeiten an den Zellecken und Berücksichtigung des Überschreitens der
Flamme über Zellecken
7.7 Literatur
[1] R.D.
Richtmyer, K.W. Morton: „Difference Methods for Initial Value Problems“, 2nd
Edition, Interscience, New York, 1967
[2] P.J.
Roache: „Computational Fluid Dynamics“, Hermosa, Albuquerque, New Mexico, 1972
[3] S.V.
Patankar: „Numerical Heat Transfer and Fluid Flow“, Hemisphere, Washington,
D.C., 1980
[4] R.
Peyret, T.D. Taylor: „Computational Methods for Fluid Flow“, Springer, New
York, 1983
[5] D.A.
Anderson, J.C. Tannehill, R.H. Pletcher: „Computational Fluid Mechanics and
Heat Transfer“, Hemispheere Publishing Corporation, New York, 1984
[6] C.
Hirsch: „Numerical Computation of Internal and External Flows“, Vol. 1 Fundamentals
of Numerical Discretization, Wiley Sons: Chichster, New York, 1988
[7] C.
Hirsch: „Numerical Computation of Internal and External Flows“, Vol. 2 Computational
Methods for Inviscid and Viscous Flows, Wiley Sons: Chichster, New York, 1988
[8] U.
Bielert, M. Klug, G. Adomeit: „Numerical Simulation of the Turbulent Combustion
Process in a Rapid Compression Device“, SAE Paper 940211, 1994
[9] U. Bielert: „Numerische Simulation
turbulenter Verbrennungsvorgänge unter motorischen Bedingungen mit einem Front
Tracking Verfahren“, Fortschr.-Ber. VDI Reihe 12 Nr. 223
[10] U.
Bielert, M. Klug, G. Adomeit: „Application of Front Tracking Techniques to the
Turbulent Combustion Processes in Single Stroke Engine“, Combustion and Flame, 1996
[11] V.
Smiljanovski, R. Klein: „Flame Front Tracking via In-cell Reconstruction“,
Proceedings of the Fifth International Conference on Hyperbolic Problems,
Theory, Numerics, and Applications, Stony Brooks, New York, 1995.
[12] V.
Smiljanovski, R. Klein: „Simulation of Gasdynamic Flame Instability and DDT
Using In-cell Reconstruction“, Proceedings of the Sixth International Symposium
on Computational Fluid Dynamics, Lake Tahoe, Nevada, September 4-8, 1995
[13] D.
Adalsteinsson, J.A. Sethian: „A Fast Level Set Method for Propagating
Interfaces“, Journal of Computational Physics 118, 269-277, 1995
[14] V. Smiljanovski: „Ein numerisches
Verfahren zur Berechnung schneller Vormischflammen und der Deflagrations-Detonations-Transition
(DDT)“, Dissertation RWTH Aachen, 1996
[15] P.D.
Thomas, C.K. Lombard: „Geometric Conservation Law and Its Application to Flow
Calculations on Moving Grids“, AIAA, 17, 1979
[16] Y.
Tamura, K. Fujii: „Conservation Law for Moving and Transformed Grids“, 11. AIAA
Computational Fluid Dynamics Conference, 6-9 July, 1993
[17] K. Dortmann: „Numrische Simulation
instationärer Profilumströmungen“, Dissertation, RWTH Aachen, 1989
[18] M.G.
Hall: „Cell-vertex multigrid schemes for solution of the Euler equations“,
Numerical methods for fluid dynamics II, Eds K,W. Morton and M.J. Baines, Clarendon
Press, 303-345, 1986
[19] G.
Strang: „On the Construction and Comparison of Difference Schemes“, SIAM, J.
Num. Anal., 5, 506-517, 1968
[20] P.D.
Lax, B. Wendroff: „Systems of conservation laws“, Comm. Pure and Appl. Math.,
13, 217-237, 1960
[21] A.
Harten, P.D. Lax, B. van Leer: „On upstream differencing and Godunov-type schemes
for hyperbolic conservation laws“, SIAM Rev., 25, 35-62, 1983
[22] B.
Einfeldt: „On Godunov-Type Methods for Gas Dynamics“, SIAM, J. Num. Anal.,
25, No. 2, 1988
[23] B. Einfeldt: „Zur Numerik der
stoßauflösenden Verfahren“, Dissertation, RWTH Aachen, 1988
[24] S.K.
Godunov: „Finite-Difference Method for Numerical Computation of Discontinuous
Solutions of the Equations of Fluid Dynamics“, Mat. Sbornik 47, 271-306, 1959
[25] P.L.
Roe: „Approximate Riemann-Solvers, Parameter Vectors and Difference Schemes“,
J. Comp. Phys., 43, 357-372, 1981
[26] A.
Harten: „High Resolution Schemes for Hyperbolic Conservation Laws“, J. Comp. Phys.,
49, 357-393, 1983
[27] P.K.
Sweby: „High resolution schemes using flux limiters for hyperbolic conservation
laws“, SIAM J. Num. Anal., 21, pp. 995-1011, 1984
[28] A.
Harten: „On a class of high resolution total-variation-stable finite-difference
schemes“, SIAM J. Numer. Anal., 21, 1-23, 1984
[29] R.
Courant, K.O. Friedrichs: „Supersonic Flows and Shock Waves“, Interscience Publishers,
New York, 1948
[30] J.M.
Hyman: „Numerical Methods for Tracking Interfaces“, Physica 12D, 12: 396-407,
1984, North-Holland, Amsterdam
[31] W.T.
Ashurst, P.K. Barr: „Stochastic Calculation of Laminar Wrinkled Flame Propagation
via Vortex Dynamics“, Comb. Sci. and Tech. 34:227-256, 1983
[32] P.K.
Barr: „Acceleration of a Flame by Flame-Vortex Interactions“, Combustion and
Flame 82:111-125, 1990
[33] A.J.
Chorin: „Flame Advection and Propagation Algorithms“, Journ. of Comp. Physics
25:253-272, 1977
[34] A.J.
Chorin: „Random Choise Methods with Application to Reacting Gas Flow“, Journ.
of Comp. Physics 25:253-272, 1977
[35] A.J.
Chorin: „Random Choise Solution of Hyperbolic Systems“, Journ. of Comp. Physics
22:517-533, 1976
[36] E.G.
Groff: „An Experimental Evaluation of an Entrainment Flame-Propagation Model“,
Combustion and Flame 67:153-162, 1987
[37] E.
Tomita, Y. Hamamoto: „The Effect of Turbulence on Combustion in Cylinder of
Spark-Ignition Engine - Evaluation of Entrainment Model“, SAE Paper 880128,
1988
[38] C.W.
Hirt, B.D. Nichols: „Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries“,
Journ. of Comp. Physics 39:201-225, 1981
[39] N.
Ashgriz, J.Y. Poo: „FLAIR: Flux Line-Segment Model for Advection and Interface
Reconstruction“, Journ. of Comp. Physics 93:449-468, 1991
[40] W.F.
Noh, P. Woodward: „SLIC (Simple Line Interface Calculation)“, in Lecture Notes
in Physics, vol. 59; Proc. Fifth. Int. Conf. on Numerical Methods in Fluid
Dynamics, A.I. van de Vooren and P.J. Zandbergen, eds. (Springer-Berlin), 1976
[41] P.K.
Barr, W.T. Ashurst: „An Interface Scheme for Turbulent Flame Propagation“,
Sandia Report SAND82-8773, Sandia National Laboratories, 1982
[42] R.J.
Tabaczynski, F.H. Trinker, B.A.S. Shannon: „Further Refinement and Validation
of a Turbulent Flame Propagation Model for Spark-Ignition Engines“, Combustion
and Flame 39:111-121, 1980
[43] W.T.
Ashurst: „The Structure of Turbulence and Its Effect Upon Flames“, Lecture at
the ERCOFTAC Summer School, European Research Community On Flow Turbulence And
Combustion, Aachen, 1992
[44] A.F.
Ghoniem, O.M. Knio: „Numerical Simulation of Flame Propagation in Constant
Volume Chambers“, 21st Symp. (Int.) on Combustion, 1313-1320, 1986
[45] J.
Sethian: „Turbulent Combustion in Open and Closed Vessels“, Journ. of Comp. Physics
54:425-456, 1984
[46] A.F.
Ghoniem, A.J. Chorin, A.K. Oppenheim: „Numerical Modeling of Turbulent Combustion
in Premixed Gases“, 18th Symp. (Int.) on Combustion, 1375-1383, 1981
[47] R.J.
Cattolica, P.K. Barr, N.N. Mansour: „Propagation of a Premixed Flame in a Divided-Chamber
Combustor“, Combustion and Flame 77:101-121, 1989
[48] P.K.
Barr, P.O. Witze: „Some Limitations to the Spherical Flame Assumption Ised in
phenomenological Engine Models“, SAE Paper 880129, 1988
[49] I.
Chern, P. Colella: „A conservative front tracking method for hyperbolic
conservation laws“, Preprint UCRL-97200, Lawrence Livermore National
Laboratory, 1987
[50] A.
Bourlioux: „Numerical Study of Unstable Detonations“, Dissertation, Princeton
University, Juni 1991
[51] A.
Bourlioux, A. Majda: „Theoretical and Numerical Structure for Unstable
Two-Dimensional Detonations“, Combustion and Flame, 90, 211-229, 1992
[52] S.
Osher. J.A. Sethian: „Fronts Propagating with Curvature-Dependent Speed: Algorithms
Based on Hamilton-Jacobi Formulations“, Journal of Computational Physics, 79,
12-49, 1988
[53] J.A.
Sethian: „Curvature and the Evolution of Fronts“, Commun. Math. Phys., 101,
487-499, 1985
[54] C.
Rhee, L. Talbot, J.A. Sethian: „Dynamical Behavior of a Premixed Turbulent Open
V-Flame“, Report PAM-599, Center for Pure and Applied Mathematics, University
of California, Berkeley, January 1994
[55] C.
Rhee, L. Talbot, J.A. Sethian: „Dynamical Study of a Premixed V flame“, Jour. Fluid
Mech., 300, pp.87-115, 1995
[56] R.J.
LeVeque, K.M. Shyue: „Shock Tracking Based on High Resolution Wave Propagation
Methods“, Research Report No. 91-02, February 1992, Department of Applied Mathematics,
University of Washington
[57] K.M.
Shyue: „Front Tracking Methods Based on Wave Propagation“, Research Report No.
93-02, June 1993, Department of Applied Mathematics, University of Washington
[58] R.J.
LeVeque: „A large time step generalization of Godunov's method for Systems of
conservation laws“, SIAM J. Numer. Anal., 22, pp. 1051-1073, 1985
[59] R.J.
LeVeque: „Shock tracking with the large time step method“, in Proc. 7th Intl. Conf.
Comput. Meth. in Appl. Sci. Eng., R. Glowinski and J.-L. Lions, eds.,
Versailles, 1985
[60] R.J.
LeVeque: „High Resolution Finite Volume Methods on Arbitrary Grids via Wave
Propagation“, J. Comp. Phys., 78, 36-63, 1988
[61] Z.H.
Teng, A.J. Chorin, T.P. Liu: „Riemann Problems for Reacting Gas“, with Application
to Transition, Siam J. Appl. Math, Vol. 42, No. 5, October 1982
[62] F.A.
Williams: „Turbulent combustion“, in The Mathematics of Combustion, J.D. Buckmaster
(ed.), SIAM, 97-131, 1985
[63] M.
Sussman, P. Smereka, S. Osher: „A Level Set Approach for Computing Solutions to
Incompressible Two-Phase Flow“, Journal of Computational Physics, 114, 146-159,
1994
[64] M.
Sussman, E. Fatemi, P. Smereka, S. Osher: „A Level Set Approach for Computing
Solutions to Incompressible Two-Phase Flow II“, Proceedings of the Sixth
International Symposium on Computational Fluid Dynamics, Lake Tahoe, Nevada,
September 4-8, 1995
Webseite aktualisiert am 21.08.2001
/ Yvonne Lennartz
![]() wird hervorgerufen
durch konvektive und diffusive tensorielle Flüsse
wird hervorgerufen
durch konvektive und diffusive tensorielle Flüsse ![]() über die Oberfläche
des Gebietes und zum Beispiel durch Quellen und Senken im Inneren
über die Oberfläche
des Gebietes und zum Beispiel durch Quellen und Senken im Inneren ![]() des Gebietes. Die
allgemeine mathehmatische Formulierung lautet mit dem nach außen gerichteten
Vektor
des Gebietes. Die
allgemeine mathehmatische Formulierung lautet mit dem nach außen gerichteten
Vektor ![]() des Oberflächenelementes
des Oberflächenelementes![]() der konservativen Variablen
und den konvektiven und diffusiven Flüssen auf
der konservativen Variablen
und den konvektiven und diffusiven Flüssen auf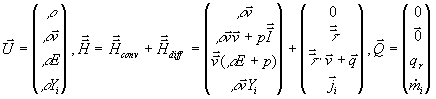 .
.![]() den
Geschwindigkeitsvektor,
den
Geschwindigkeitsvektor, ![]() die spezifische
innere Totalenergie, p den Druck sowie
Yi die Massenbrüche und
die spezifische
innere Totalenergie, p den Druck sowie
Yi die Massenbrüche und ![]() die
Bildungsenthalpien der Spezies i.
die
Bildungsenthalpien der Spezies i.![]()
![]() .
.![]() ,
,![]() die stöchiometrischen
Nettokoeffizienten (netto) von Spezies i
in der Reaktion k mit der
Reaktionsrate wk bezeichnen.
die stöchiometrischen
Nettokoeffizienten (netto) von Spezies i
in der Reaktion k mit der
Reaktionsrate wk bezeichnen.![]()
![]()
![]() für
für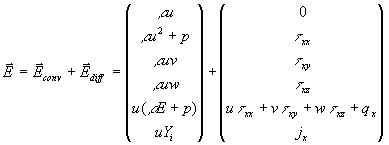 .
.![]()
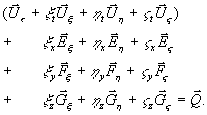
![]() und zum Beispiel
und zum Beispiel ![]() . Darin ist J die
Funktionaldeterminante der Transformation
. Darin ist J die
Funktionaldeterminante der Transformation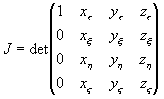 .
.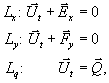

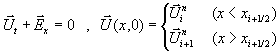


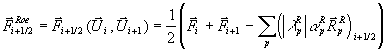 .
.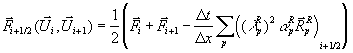 .
.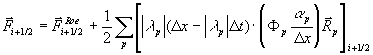
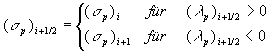





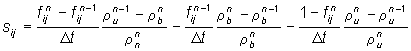



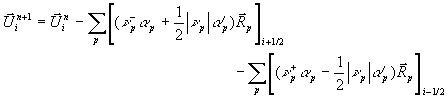
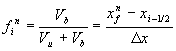

 .
.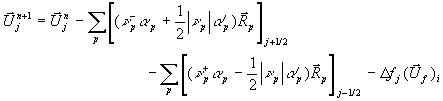
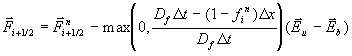 .
.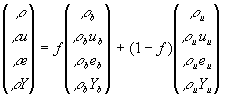
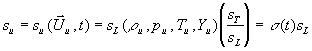 ,
,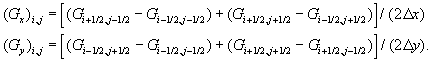

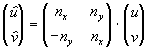 .
.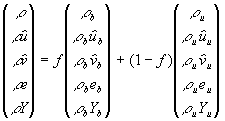
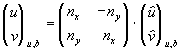 .
.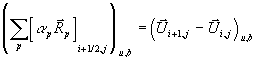 .
.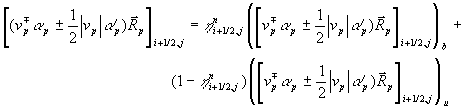
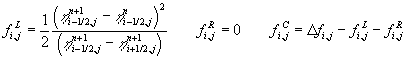 .
.